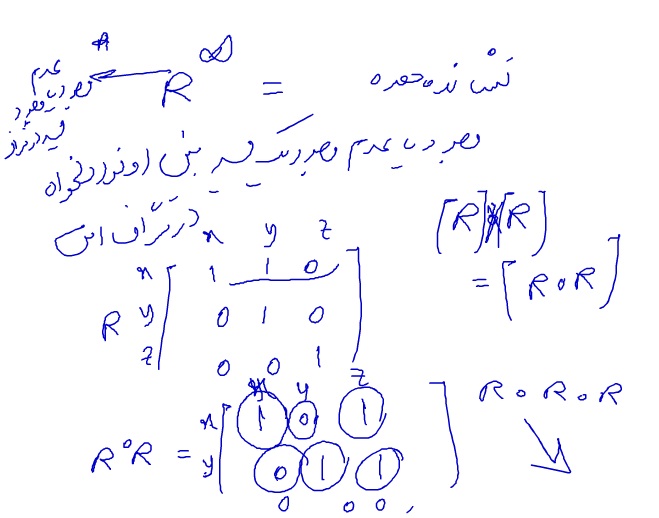
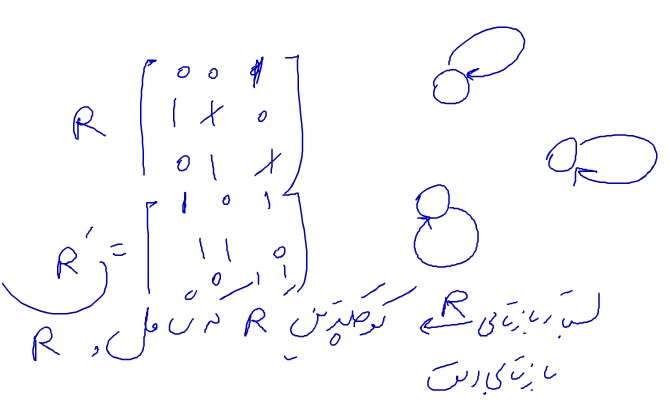
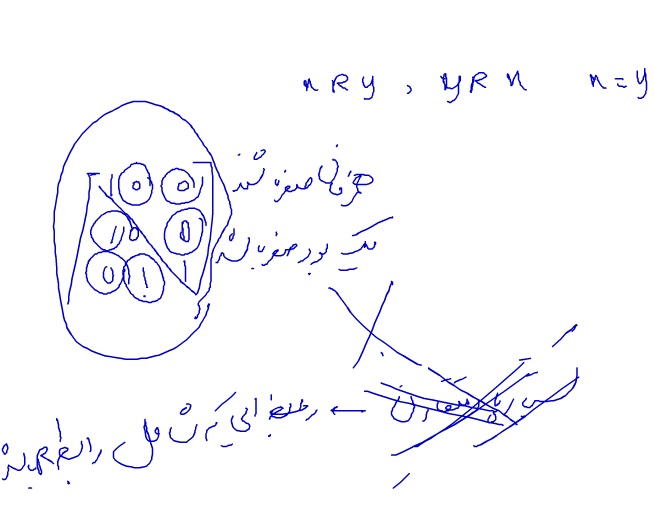
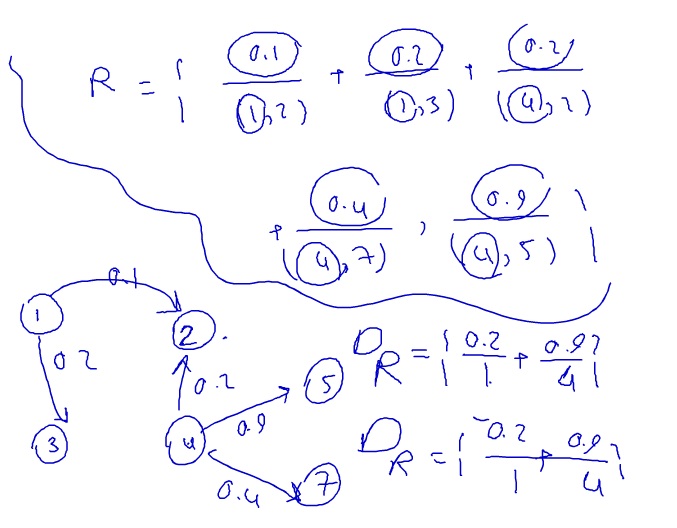
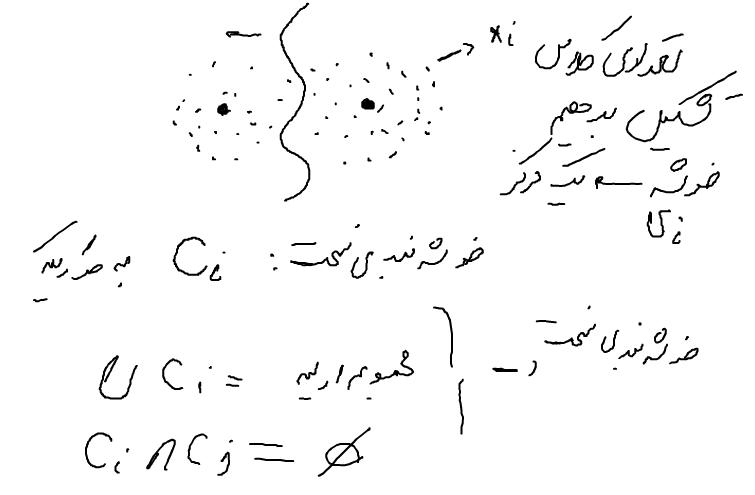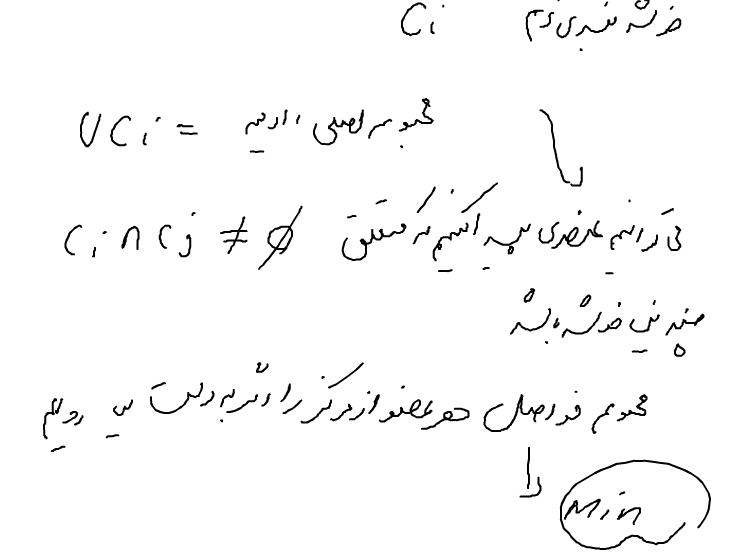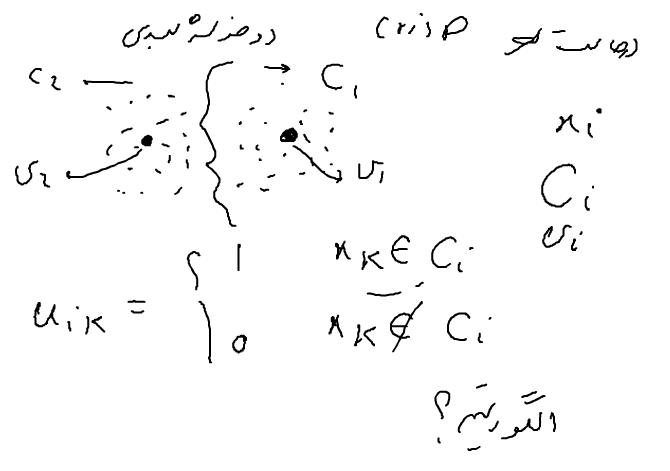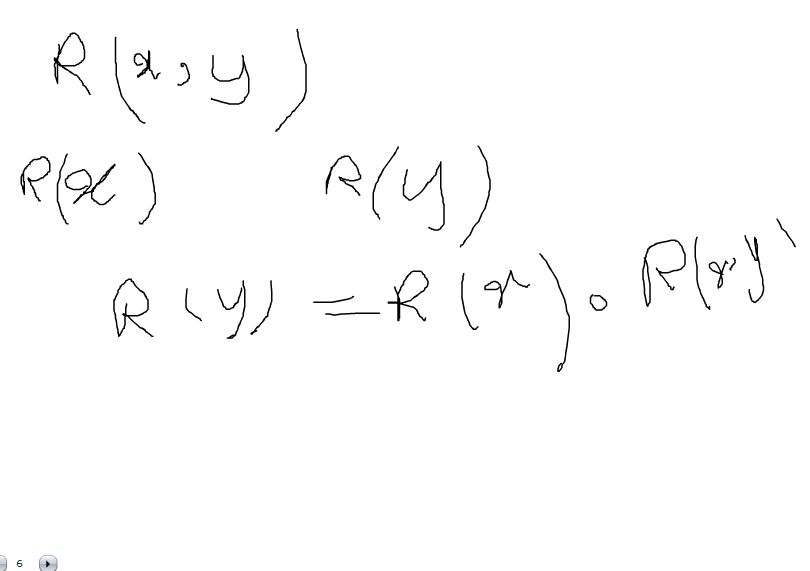درخت تصمیم
FCL
خوشه بندی فازی
با استفاده از روال های آموزشی یک سری قوانین را تشخیص می دهند
ژنتیک و شبکه عصبی درابتدا باید در یک بازه آموزشی Learn شوند و if then rule ها را بسازند
درخت تصمیم : فرض کنیم ماشینی طراحی کردیم که می خواهد سیب ها را از پرتقال ها
جدا کند بر اساس ۴ مشخصه ( قند – رنگ – سفتی – وزن چگالی)
از این چهار خصوصیت ، دو خصوصیت برتر را مشخص می کنیم ( بهره اطلاعاتی )
مثلا خصوصیت سفتی بهره اطلاعاتی بیشتری دارد
سپس خصوصیتی که بهره اطلاعاتی بعدی را دارد شاخه های بعدی را تشکیل می دهند
بر این اساس درخت ایجاد شده بدست می آید
حالا بر اساس برگ های درخت Rule ها ایجاد شده اند
احتمال درست بودن هریک از برگ ها به صورت فازی مشخص می شوند
حالا که بر اساس داده های Train درخت تصمیم را ساختیم
مرحله بعدی داده های Test را به آن می دهیم
ممکن است بعضی از اطلاعات به صورت Crisp باشد و برخی دیگر به صورت Fuzzy
– اگر تعداد خصوصیت ها زیاد باشد درخت تصمیم خیلی بزرگ می شود
از تکنیک های هرس باید استفاده کنیم
و یا راهکار feature Selection استفاده می کنیم
—————-
برای تمرین یک سری داده بیاورد که از روی آن درخت تصمیم بسازیم
—————–
انواع درخت های تصمیم خیلی زیاد هستند ( C4 , C5 , Kart, ID3
در اینجا از درخت تصمیم نوع FID3 استفاده می کنیم
هرخصوصیت را A1 تا An می گیریم
هر خصوصیت می تواند چند تا مقدار داشته باشد A1mو A2m و A3m
بهره اطلاعاتی با از A1 تا An می سنجیم (می توان با استفاده از آنتروپی شانون بهره اطلاعاتی را سنجید)
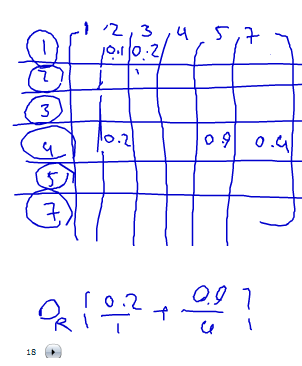
و همچنین با روش زیر : کاردینالیتی مجموعه های فازی – که کل مقادیر تعلق را با هم جمع می کنیم )
به ازای هر کلاس Ti را تعریف می کنیم که به آن می گوییم اطلاعات ترکیبی تکمیلی
Cardinality
بهره اطلاعاتی : میزان اطلاعاتی که با توجه به آن خصوصیت بدست می آید
در این جدول مثال ۴ خصوصیت داریم که
برای A1 سه حالت داریم
برای A2 سه حالت داریم
برای A3 دو حالت داریم
و برای A4 دو حالت داریم
برای خروجی B1 هم سه حالت داریم
در این جدول مثلا ۱۰۰۰ رکورد اطلاعات داریم که با ۳۰۰ تای آن درخت تصمیم را می سازیم ( شکل می دهیم ) و با ۴۰۰ تای آن تست می کنیم
ابتدا ریشه درخت را بر اساس خصوصیتی که بهره اطلاعاتی بیشتری دارد می سازیم
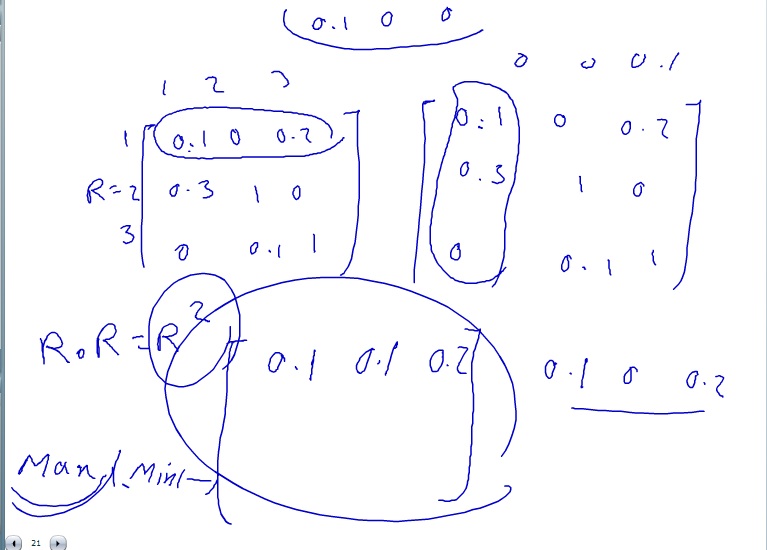
پس در اولین مرتبه بهره اطلاعاتی I(B|A1) و I(B|A2) و I(B|A3) و I(B|A4) را محاسبه می کنیم
ماکزیمم آن ها را به عنوان ریشه درخت در نظر میگیریم
هرس :
می توانیم شاخه های درخت را هرس کنیم
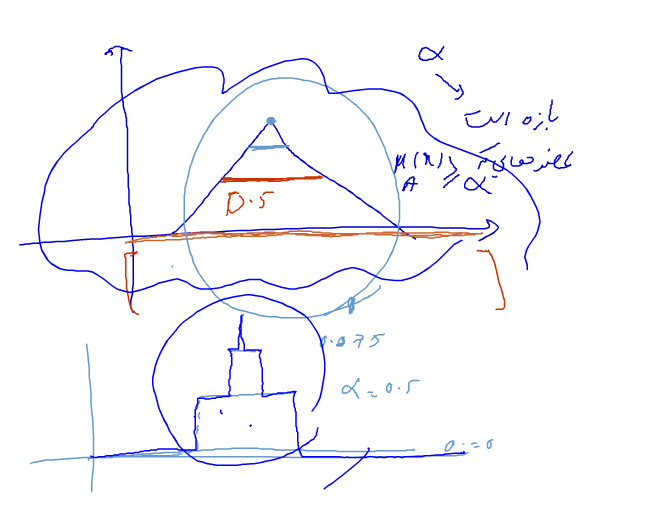
معیار هرس : اگر درصد یکی از کلاس ها یک مقداری کمتری بود( minimum support ) دیگر آن شاخه را ادامه نمی دهیم
اگر بدون هرس کردن بخواهیم درخت تصمیم را بسازیم خیلی بزرگ می شود
هر چقدر بخواهیم دقیق تر باشد بتا را بیشتر می کنیم
اگر فرکانسی جواب با f نمایش می دهیم کمتر از ۰/۲۵ باشد ادامه نمی دهیم
گفتیم که به ازای تک تک برگ های درخت تصمیم قانون بوجود می آید
در این درخت مثال ۲۷ قانون بدست آوردیم
شیوه بدست آوردن Bi را اینجا آورده شده است