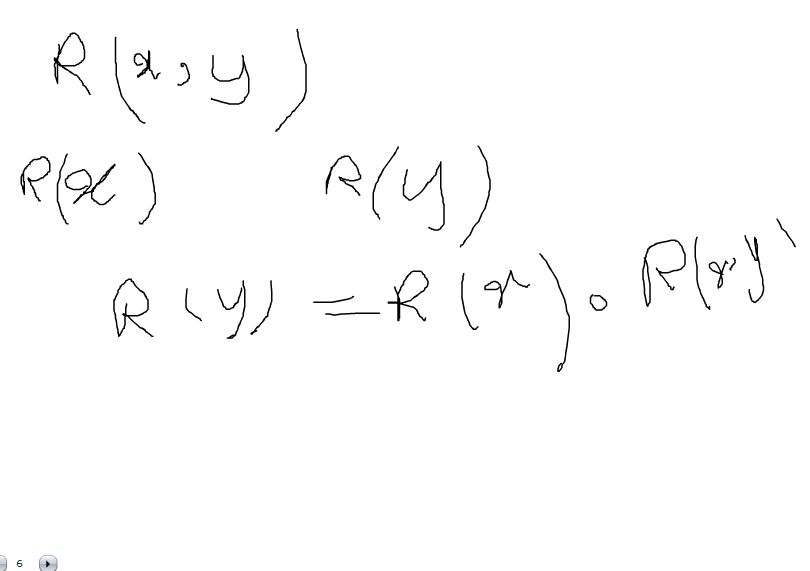از فصل ۱ تا ۷ به مقدمات نظریه های فازی می پرداخت
اما از فصل ۸ به بعد با کاربرد های فازی سر و کار داریم برای مسایل پیچیده از کاربرد فازی استفاده می کنیم
استنتاج از یکسری اطلاعات که به صورت if then بیان می کنیم و یک سری گزاره ها نتیجه گیری درست را انجام دهیم
مثال : ” اگر امروز هوا سرد است پس لباس گرم بپوش ”
یک سری فرض داریم و یک سری قوانین که بر اساس آنها نتیجه می گیریم
اگر قانونی داشته باشیم p آنگاه q و فرض ما p باشد پس q را نتیجه می گیریم
هر گزاره شرطی با نقیض خودش هم ارز است
قیاس تعدی :
p–>q و q–>r پس p–>r
اگر a جزء یک مجموعه فازی باشد آنگاه b هم جز< مجموعه فازی باشد
فرض می کنیم نمودار یک تابع را داریم
محور x ها و محور y ها
اگر نقاط x و y آن را پیدا کنیم
f(x)
از گسست و پیچش رابطه بدست می آوریم
۲ تا ترکیب مهم داریم : ممدانی – لارسن
هر قانون یک رابطه است
حالا می خواهیم در مورد R y تصمیم گیری بکنیم
در فصل ۸ یک قانون بسیار مهم هست که نیاز استنتاجی در حالت کلی GMP
هست

ورودی را با خروجی ترکیب کن میشه خروجی
…
ترکیب را به دو روش می توانیم انجام دهیم :
به دو روش Max min برای ممدانی
یا Max.Dot product برای لارسن
هر گزاره دو بخش دارد مقدم (فرض) ، تالی ( نتیجه )
به هر کدام از if then rule ها یک دلالت فازی ( implication ) می گوییم
خود این if then rule ها رابطه هستند
رابطه ها نتیجه حاصلضرب کارتزینی هستند
اسلاید ۱۱
Fuzzy Implications
هر rule را می توانیم به صورت گسست فازی یا پیچش فازی تعریف کنیم
مینی مم –> پیچش –> ممدانی
ماکزیمم دات –> پیچش –> لارسن
اکر یک rule داشته باشیم بر دلالت فازی اگر بینش بجای اشتراک مینی مم بگذارم
پیچش ممدانی می شود و اگر دات بگذاریم ، پیچش لارسن می شود
گسست بین دو مجموعه اجتماع است
پیچش بین دو مجموعه اشتراک است
اگر دما باشد آنگاه رطوبت نسبتا بالاست
دما = x
نسبتا بالا = یک ترم زبانی است
این دلالت فازی یک if then rule هست
MIMO
جعبه سیاه ما یک سری rule هستند
از هر کدام از قوانین که به دو نوع تقسیم می شدند ( mamdani – larsen )
۵ تا قضیه داریم : که با استفاده از آنها استنتاج ها را بدست می آوریم :
۱- اگر یک rule داشته باشیم که وردویش یکتایی باید و خروجی یکتایی باشد ،
ورودی یک عدد است rule را تفسیر می کنیم ( یا دلالت ممدانی یا دلالت لارسن )
ورودی را داریم به ممدانی یا لارسن می دهیم و خروجی را می گیریم
قانون دوم :
اگر دلالت فازی داشته باشیم ورودی عدد نباشد و فازی باشد
ورودی با جعبه سیاه ترکیب می کنیم و خروجی را بدست می آوریم
قانون سوم :
یک مجموعه ای از Rule ها داریم ، هر کدام از قانون ها یک ورودی داریم و یک
خروجی
خروجی می شود اجتماع ناشی از تک تک rule ها
پایگاه قوانین که خیلی rule دارد ، روی خروجی ها اجتماع می گیریم
MISO
قانون چهارم :
پایگاه دانش مجموعه از قوانین است که mIsO تعریف شده اند
به ازای هر کدام از قوانین که دو ورودی دارند و یک خروجی
حالت کلی است که بین تمامی خروجی ها اشتراک می گیریم
قانون پنجم :
اصل کار GMP است
پایگاه دانش خود را درست کنید
جعبه فازی متلب را کار کنید
اتاق ۲۱۸ – اتاق تدریس یار