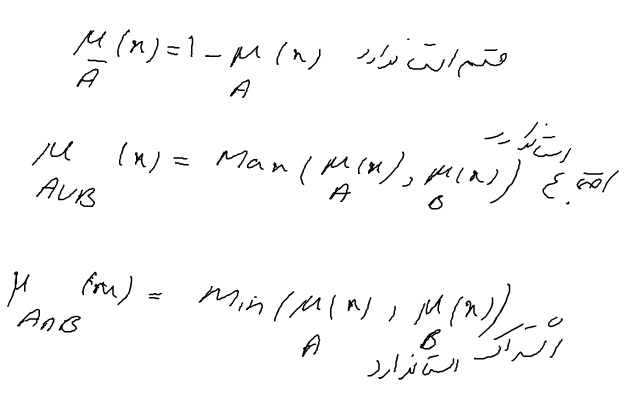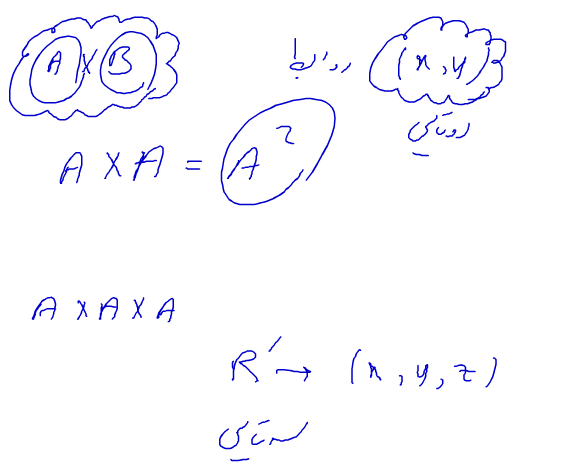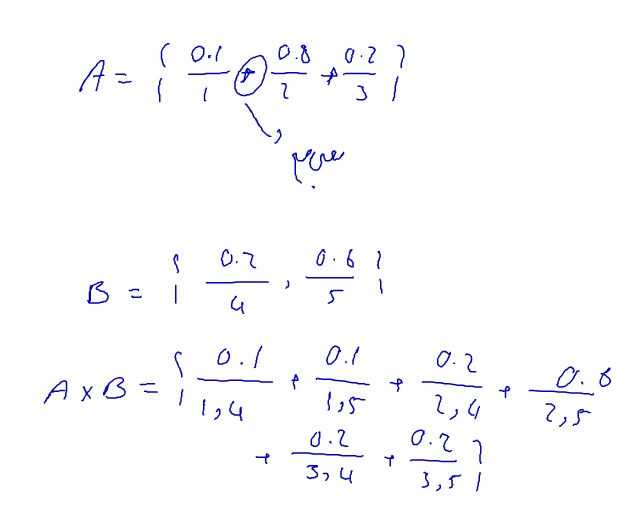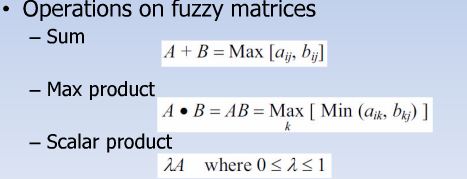باشگاه دانشجویی کارشناسی ارشد دانشگاه امیرکبیر

تمامی x هایی که میوی X آنها
آلفا کات را روی مجموعه های فازی بزنیم ، یک مجموعه ای از اعداد می شود ، به طوری که میزان تعلقیت آنها ….( میرسیم به یک بازه در اعداد کلاسیک )

می خواهیم بدانیم آلفا کات ها چه خاصیت هایی دارند
بر روی اعداد فازی عملیات های جمع و تفریق را می خواهیم انجام دهیم

ابتدا بر روی باز ه ها عملیات جمع را انجام میدهیم

می توانیم مینی مم و ماکزیمم هم روی بازه ها تعریف کنیم
آلفا کات ها که یک بازه هستند پس روی آلفا کات ها می توانیم عملیات جمع و ضرب و تفریق و تقسیم و مینیمم و ماکزیمم تعریف کنیم

عملیات روی اعداد فازی :
جمع دو عدد فازی : اگر A , B فازی باشند A+B یک مجموعه فازی می شود که اجتماع اشتراک آنها می شود

انواع اعداد فازی :

۱- عدد فازی مثلثی : به صورت مثلث تعریف می شود A(a,b,c)

مثال جمع روی عدد فازی مثلثی :

جواب ضرب و تقسیم دو عدد فازی یک عدد فازی مثلثی نمی شود

به غیر از اینها هر عملیات دیگری بخواهیم انجام دهیم باید برای آنها آلفا کات بزنیم

———————

عدد فازی ذوزنقه ای

عدد فازی گوسی – زنگوله ای
———————

گروه بندی برای پروژه انجام دهید
گروه دو نفره
چند تا مقاله انتخاب کنید
هر گروهی ۳ تا مقاله باید داشته باشد
که با پروژه ای که در محیط کارتان هست تناسب داشته باشد

مثلا درخت تصمیم فازی

———————
تمرین ها را روی کاغذ بنویسید و در جلسه حضوری بیاورید 

مجموعه های فازی را تعریف کردیم

فازی با مجموعه ها ارتباط تنگاتنگی دارد
به ازای هر عضو از مجموعه های فازی ، میزان تعلقیت خاصی بین ۰ و ۱ در نظر گرفتیم

مجموعه های Crisp به عنوان زیر مجموعه ا ی از مجموعه های فازی هم قابل تعریف است

اجتماع ، اشتراک و متمم

برای مجموعه های فازی تعداد زیادی می توانیم اجتماع ، اشتراک و متمم تعریف کنیم

پایه ای ترین آنها اجتماع ، اشتراک و متمم استاندارد هستند.

متمم به عنوان مقدار عضویت A = مقدار ۱ منهای مقدار عضویت A

اجتماع استاندارد : …
اشتراک استاندارد : مینیمم …

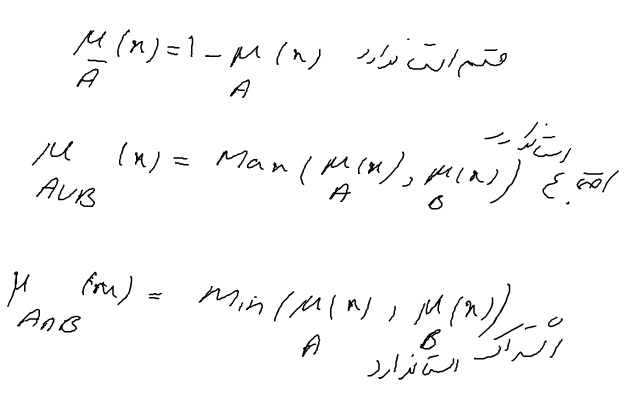
اجتماع استاندارد کوچکترین اجتماعی هست که روی اعداد فازی تعریف می شود
اشتراک استاندارد بزرگترین اشتراکی است که ر روی اعداد فازی تعریف می شود

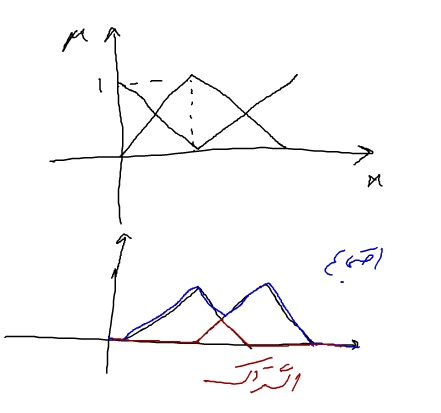
اجتماع دراستیک بزرگترین اجتماع هست
و اشتراک دراستیک کوچکترین اشتراک هست

اولین عملگر روی مجموعه های Crisp ضرب روی مجموعه ها بود

اصل گسترش :
حاصلضرب کارتزین برای مجموعه های معمولی

رابطه : هر زیر مجموعه حاصلضرب کارتزینی یک رابطه را تشکیل میدهد

هر رابطه عضوهایش :
عضو اول رابطه خاصی را رابطه دوم داریم

همکلاسی ها : مجموعه …
تعریف حاصلضرب کارتزینی :
اگر n تا مجموعه داشته باشیم و یک عضو به نام x
که میزان تعلقیت x به مجموعه را با مو نشان بدهیم
مینیمم درجه عضویت آن عضو به آن مجموعه ها است

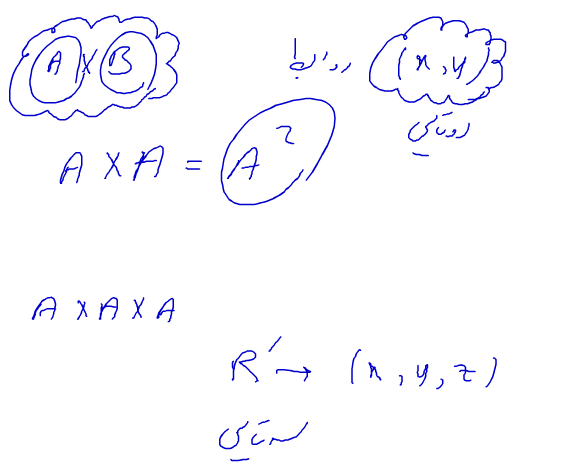
مجموع میزان تعلقیت آنها الزاما ۱ نمی شود

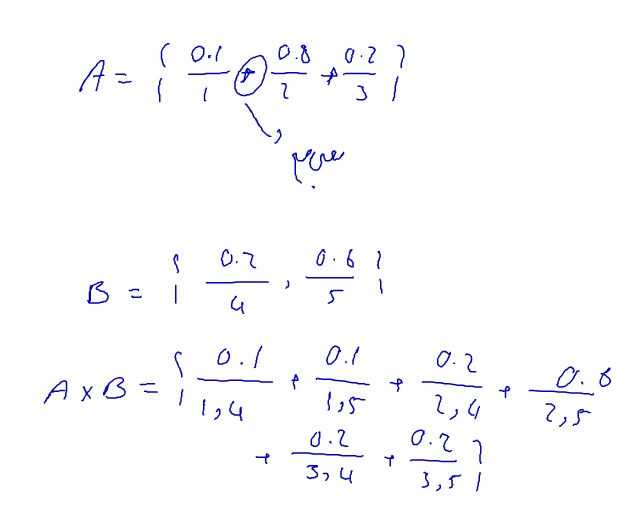
یک رابطه به صورت یک به چند هست

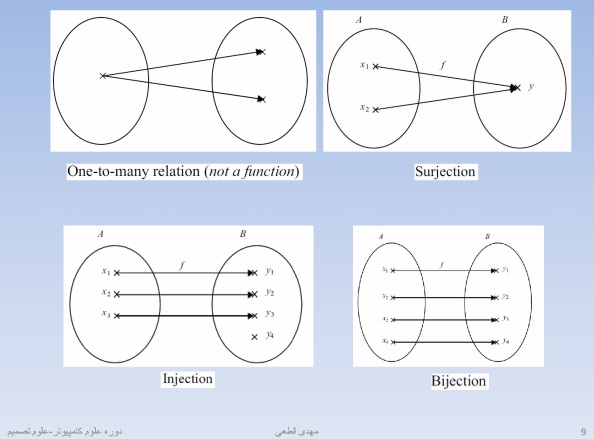
در ریاضیات کریسپ اگر x با y رابطه دارد می توانیم با گراف جهت دار آنرا نمایش بدهیم
علاوه بر گراف جهت دار با ماتریس هم در ریاضیات Crisp می توانستیم نمایش بدهیم
تعداد عضو ها برابر تعداد یال ها هست
تعداد عضو ها در ماتریس برابر تعداد درایه های ۱ هست

رابطه ها یک زیر مجموعه ای از حاصضرب کارتزینی هستند
روی رابطه ها می توانیم اشتراک ، اجتماع ، متمم داشته باشیم
معکوس رابطه را با R اینورس نمایش می دهیم

عملگر ترکیب در رابطه ها :

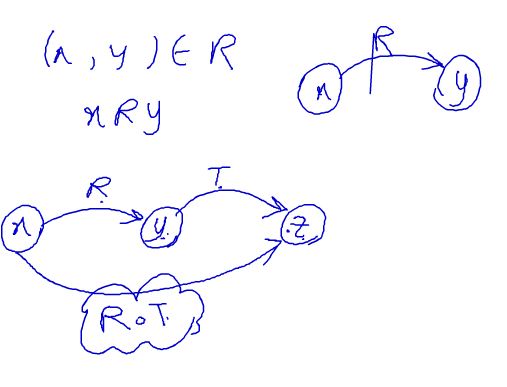
طول مسیر برابر با تعداد یال ها است

اگر بین هر دو نود یک گراف بتوان یال پیدا کرد ، می گوییم قویا متصل
اگر بین دو نود به صورت یک طرفه وجود داشته باشد ، متصل ضعیف می گوییم .

هر رابطه ای می تواند با خودش ترکیب شود

رابطه R یعنی ارتباط بین دو نود
x , y با هم که ارتباط دارند
R2 مسیر دو تای
R بتوان ب نهایت : نشان دهنده وجود یا عدم وجود مسیر بین دو نود دلخواه در گراف است

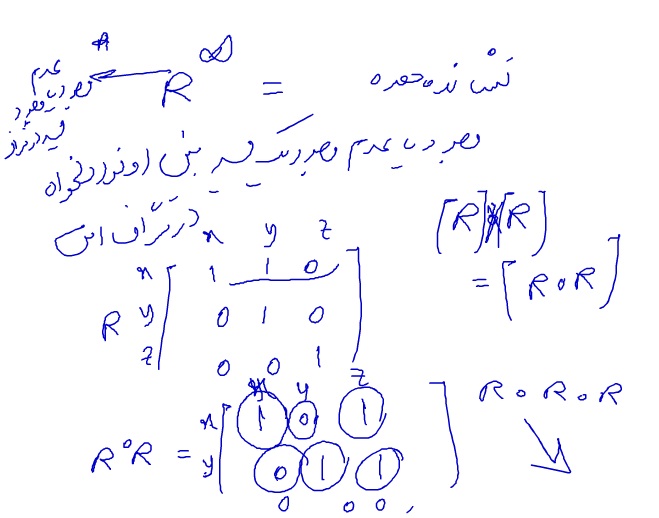
اگر بخواهیم رابطه R بتوان بی نهایت را بدست بیاوریم باید R را n-1 بار با خودش ضرب کنیم

R بی نهایت نشاندهنده وجود یا عدم وجود مسیر بین تمام نود ها هست

رابطه ها خاصیت های مختلی دارند
Reflexive – بازتابی :
Symmetric – تقارنی :

بستار بازتابی : کوچکترین رابطه ای هست مثل ‘R که شامل R هست و یک رابطه را کم دارد تا تازتابی شود
حداقل رابطه ای شامل R هست و شامل رابطه اولیه باشد

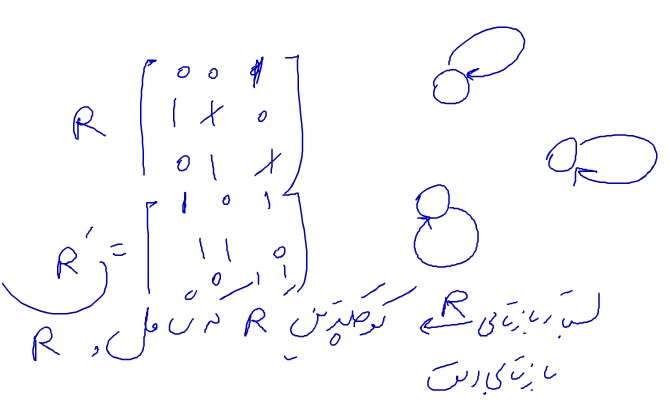
عناصر قطر اصلی که یک باشند فقط تقارنی بودن را نشان می دهند

رابطه تعدی روی گراف خیلی سخت است ، روی ماتریس هم سخت است

اگر x با y و y با z و x با z رابطه داشته باشد

اولین تمرین :
از روی یک ماتریس رابطه به چه صورت می توان به تعدی بودن آن پی برد
و از روی یک ماتریس رابطه مانند R به چه صورت می توان بستار تعدی آنرا ساخت

مهلت ارسال تمرین : سه شنبه هفته آینده
Autsoftsomputing92@gmail.com
( جواب تمرین در اسلاید ها هست )

روابط Equivalance – هم ارز هست اگر بازتابی و تقارنی و متعدی باشند

رابطه ها را می توانیم با هم ارزی کلاس بندی کنیم

با استفاده از رابطه های تلرانس عملیات

Pre order رابطه هایی بازتابی و تعدی هستند
اگر یک رابطه Pre order باشد و پاد تقارنی رابطه ترتیب -Order می شود

پس بستار پاد متقارن قابل تعریف نیست

آیا یک رابطه کوچکتر مساوی ترتیبی هست ؟

بله یک رابطه ترتیب هست
ولی رابطه کوچکتر ترتیبی نیست

———————————-
رابطه های فازی :
در رابطه های فازی می گوییم عضو ها تعلقی بین ۰ تا ۱ دارد

برای هر دامنه رابطه و برد تعریف می کنیم
دامنه R در رابطه فازی : تمامی عضو های اول را دارد و عضو دوم میزان تعلقیت آن عضو هست

در گراف : نود هایی که یال خروجی دارند در مخرج و در صورت هم ماکزیمم یال های خروجی از آن نود را می نویسیم

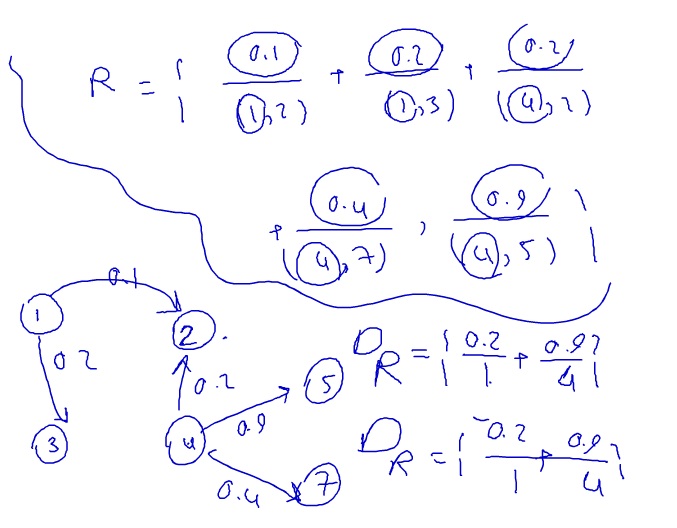
۱ و ۲ و ۳ و ۴ و ۵ و ۷ اعضای دامنه هست

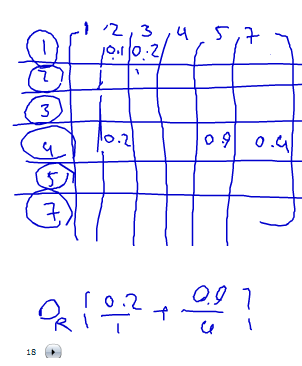
برد دامنه : روی ستون های ماکزیمم می گیریم

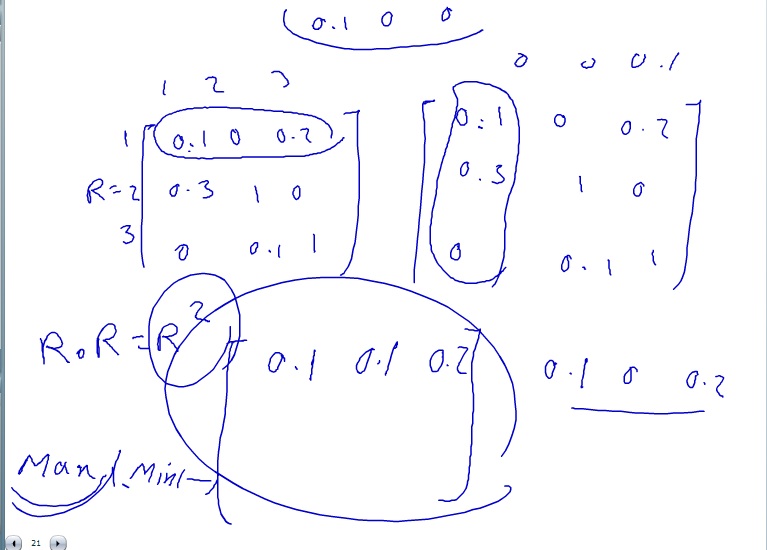
ماکزیمم – مینیمم : ترکیب است
———————————-

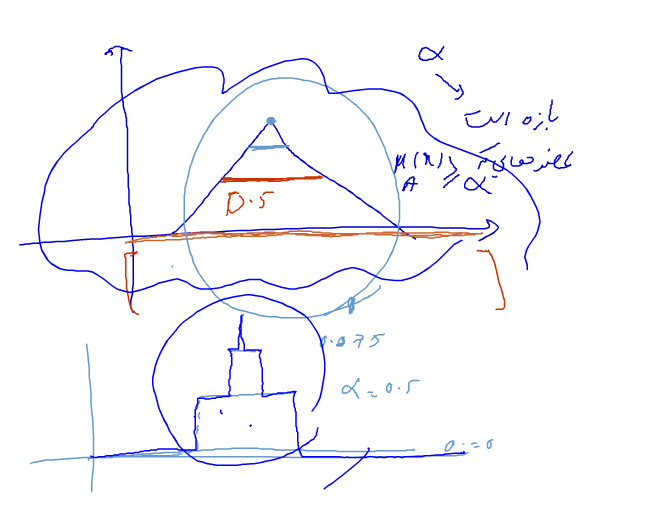
آلفا کات : تمامی عضو هایی که میزان تعلقیت آنها بزرگتر مساوی الفا هست

آلفا کات یعنی تبدیل فازی به بازه
هر چه تعداد آلفا کات ها بیشتر باشد ، به نمونه فازی مشابه تر می شود ( دقیق تر می شود )

———————————-

موضوعات پروژه را از همین الان مشخص کنید
مثلا ایمنی به صورت فازی
مقاله های فازی را بخوانید
کتاب کمکی هم بخوانید

خلاصه درس مبانی محاسبات نرم – ۹۲/۱۱/۲۶

تعبیر مجموعه های فازی با استفاده از ماتریس های فازی

با استفاده از Crisp می توانیم مجموعه های فازی را به ماتریس های فازی تبدیل کنیم

می توانیم اثر را با یک ماتریس فازی نمایش بدهیم

با درجه عضویت

عملگر جمع و ضرب داخلی ماتریس ها

آنچه که مورد نیاز است ، روابط باید بتوانند تولید اجتماع بکنند
اجتماع دو مجموعه درجه عضویت ماکزیمم دو عضو می شود.

عملگر ماکزیمم روی تک تک درایه ها استفاده می کنیم
جمع : ماکزیمم گیری درایه ها
ضرب : ماکزیمم ( مینیمم درایه ها )
ماتریس دیگری که از ماکزیمم گیری روی تمام مجموعه ها در سطر i ام و ستون j ام

در حالت اسکالر – بین صفر و یک – تمامی درجه عضویت ها در صفر و یک ضرب می شود

می توانیم برای بیش از یک رابطه هم نتیجه داشته باشیم
برای اجتماع M رابطه فازی درایه به درایه ماکزیمم گیری کنیم
برای اشتراک ، مینیمم گیری

معکوس : اگر در رابطه فازی x , y وجود داشته باشد ، درجه عضویت x , y با استفاده از این رابطه
قابلیت گسترش پیدا می کند همان درجه هست و یک نماد هست و اینورس نیست

برای مجموعه های فازی متفاوت برای ریاضیات کلاسیک هست

رابطه ای که برای دو تا مجموعه بدست آوردیم برای بیش از دو مجموعه هم تعمیم می دهیم

….
توسعه تصویری :
اگر در رابطه r 0.2 , 0.3 هم وجود داشت می توانیم نتیجه بگیریم که در رابطه های قبلی وجود داشته
توسعه تصویری
به صورت بازگشتی تصویر می کند

به صورت درایه ای هم می توانیم نگاه کنیم
می توانیم تمام درجه عضویت های MR را پیدا کنیم و cut بزنیم

همین کار را در توسعه سیلندری می توانیم داشته باشیم

توسعه سیلندری :

توسعه سیلندری معمولا نرم افزار هایی مثل متلب انجام می دهند
یک بردار داریم می خواهیم توسعه بدهیم به یک ماتریس
آنچه را که به عنوان درجه عضویت داریم …

هنگامی که رشد می دهیم به سمت بالا ، درجه عضویت ها هم رشد می کنند.

توسعه سیلندری را در چند بعد هم می توانیم گسترش دهیم
ولی در توسعه تصویری به این راحتی ها نیست

توسعه
ابتدا تابعی را در نظر می گیریم ، یک به یک و کوشا

اگر تابع پوشا باشد
اگر f(y) پوشا نباشد معکوسش هم ….

یک مثال از توسعه Extention
فرض کنیم مجموعه A و B را دارم که A غیر فازی و B فازی باشد
تک تک عنصر های B را ….

اصل توسیع را برای حالت حاصلضرب تعدادی از مجموعه بکار بردیم ، کافیست که برای تک مجموعه ها
کمترین درجه عضویت ها را …

مثال از Distance

جمع بندی :
یک رابطه خوبی بین ریاضیات کلاسیک و فاز وجود دارد
۱- مینیمم و ماکزیمم سازی
۲- راهکار خرد کردن رابطه فازی به آلفا کات ها
۳- توسعه داده فازی با ابعاد بزرگتر (Distance خیلی پر کاربرد است ) , Extention سیلندر ها برای مش ها