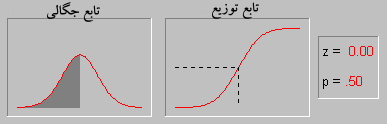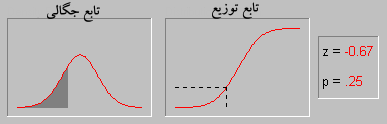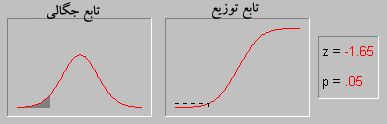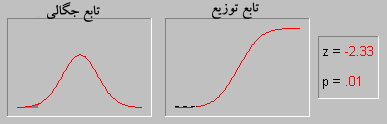
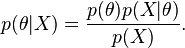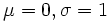۹۱/۰۲/۱۰
فصل ۸ – ژنتیک
الگوریتم زنتیک و کاربرد آن در یادگیری ماشین
تکامل طبیعی (قانون انتخاب طبیعی داروین)
الگوریتم ژنتیک
مجموعه ای از افراد داریم
هر فردی خصوصیاتی دارند
هر ژن ویژگی های خاصی را میتواند رمز کند
هر کروموزوم دارای مجموعه ای خواص ژنتیکی هست.
ساختار الگوریتم های ژنتیک
مساله –>مدلسازی مساله –> تشکیل جمعیت اولیه –> جستجوی ژنتیکی–> جواب
نحوه کدکردن مساله خیلی مهم است
چون در تمامی مراحل از همین کد و دی کد استفاده می کنیم
معمولا از روش باینری استفاده می کنیم
صفحه ۱۲ از ۳۲
بازنمایی
فضایی از مساله داریم
جمعیت ، مجموعه از راه حل ها ( کروموزوم ها )
ارزیابی جمعیت – Fitness
بهینه کردن شایستگی ها
انتخاب Selection (انتخاب والدین )
روش های انتخاب والدین :
۱- انتخاب تمام جمعیت به عنوان والدین
۲- انتخاب تصادفی
۳- روشهای دیگر
۳-۱ انتخاب مناسب ترین هر اجتماع
۳-۲ چرخ رولت – مبتنی بر شایستگی
۳-۳ Scaling Selection
۳-۴ Tournoment Selection
عملگر های الگوریتم ژنتیک
ترکیب مجدد (Crossover)
چندین روش برای ترکیب هست
۱- ترکیب تک نقطه ای ( از یک قسمت ژنوم هر کدام از والد ژنوم را تقسیم کنیم و با هم ترکیب کنیم )
۲- ترکیب دو نقطه ای ( در چند نقطه می تواند ژنوم ها ترکیب شود )
۳- ترکیب بر اساس مدل
جهش ژنتیک : اگریکی از بیت ها مخالف والدین باشد
شرط خاتمه
مزایای GA
مشکل Crowding
راه حل های Crowding :
۱- استفاده از ranking
۲- Fitness sharing
کاربرد الگوریتم ژنتیک در یادگیری ماشین
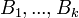 یک افراز برای فضای نمونه ای
یک افراز برای فضای نمونه ای  تشکیل دهند. طوری که به ازای هر
تشکیل دهند. طوری که به ازای هر 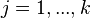 ، داشته باشیم
، داشته باشیم 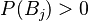 و فرض کنید
و فرض کنید  پیشامدی با فرض
پیشامدی با فرض  باشد، در اینصورت به ازای
باشد، در اینصورت به ازای 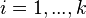 ، داریم:
، داریم:
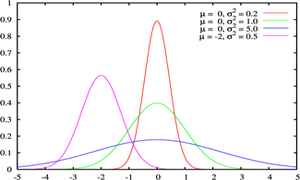
 (که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد.
(که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد. پس از مشاهده داده
پس از مشاهده داده  برابر است با
برابر است با 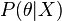 . اگر
. اگر 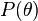 احتمال پیشین
احتمال پیشین