۹۱/۰۲/۰۷ ESL
معادله اصلی قضیه بیز
فرض میکنیم 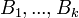 یک افراز برای فضای نمونه ای
یک افراز برای فضای نمونه ای  تشکیل دهند. طوری که به ازای هر
تشکیل دهند. طوری که به ازای هر 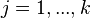 ، داشته باشیم
، داشته باشیم 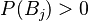 و فرض کنید
و فرض کنید  پیشامدی با فرض
پیشامدی با فرض  باشد، در اینصورت به ازای
باشد، در اینصورت به ازای 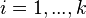 ، داریم:
، داریم:

تصمیم بیز : تصمیمی است که ریسک بیز آن کمترین باشد
تابع ریسک بیز
ریسک پسین
چگالی پیشین اطلاعاتی که از قبل داریم
چگالی پسین ، احتمال شرطی به شرط تتا
اگر تصمیم بیز داشته باشیم
ریسک پسین کمترین مقدار خودش را دارد
اگر تابع زیان درجه ۲ باشد می نیمم بیز E(teta|x) است
E(L(teta , d)
احتمال پیشین
در آمار، توزیع احتمال پیشین یک کمیت احتمالاتی مانند  (که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد.
(که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد.
کمیت احتمالاتی می تواند پارامتر یا متغیر نهان باشد.
با استفاده از قضیه بیز میتوان احتمال پیشین را در درستنمایی داده مشاهدهشده ضرب و پس از نرمالیزه کردن توزیع احتمال پسین را بهدست آورد.
احتمال پیشین کاملاً به نظر متخصص داده و آگاهی قبلی او در مورد داده بستگی دارد.
احتمال پسین
در آمار بیزی، توزیع احتمال پسین یک کمیت احتمالاتی توزیع احتمالی است پس از مشاهده شواهد (داده ). به عبارت دیگر، توزیع احتمال پسین احتمال شرطی آن کمیت است به شرط دیدن داده.
به بیان ریاضی: احتمال پسین یک پارامتر  پس از مشاهده داده
پس از مشاهده داده  برابر است با
برابر است با 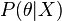 . اگر
. اگر 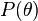 احتمال پیشین
احتمال پیشین  ، یعنی آگاهی پیشین ما در مورد
، یعنی آگاهی پیشین ما در مورد  ، را نشان دهد، با استفاده از قاعده بیز میتوان نوشت:
، را نشان دهد، با استفاده از قاعده بیز میتوان نوشت:
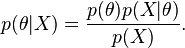
که در آن  درستنمایی داده را نشان میدهد. برای به خاطر سپردن این رابطه میتوان به صورت زیر نیز فکر کرد:
درستنمایی داده را نشان میدهد. برای به خاطر سپردن این رابطه میتوان به صورت زیر نیز فکر کرد:

برای امتحان ۱ خرداد فصل ۳ ( رگرسیون subset selection , Ridge , Lasso , PCR) و تصمیم آماری تا ابتدای تصمیم روا ( ابتدای فصل ۶ گرفته می شود.
فصل ۶ و ۷ برای پایان ترم امتحان گرفته می شود
کتاب تصمیم آماری دکتر بهبودیان را بگیرید
شماره تلفن کتابفروشی که دوستان در اختیار گذاشتند :
۶۶۴۰۵۴۰۳
۶۶۴۷۵۷۹۴
منبع : ویکی پدیا
قضیه بیز :
http://fa.wikipedia.org/wiki/%D9%82%D8%B6%DB%8C%D9%87_%D8%A8%DB%8C%D8%B2
احتمال پیشین :
http://fa.wikipedia.org/wiki/%D8%A7%D8%AD%D8%AA%D9%85%D8%A7%D9%84_%D9%BE%DB%8C%D8%B4%DB%8C%D9%86
احتمال پسین :
http://fa.wikipedia.org/wiki/%D8%A7%D8%AD%D8%AA%D9%85%D8%A7%D9%84_%D9%BE%D8%B3%DB%8C%D9%86
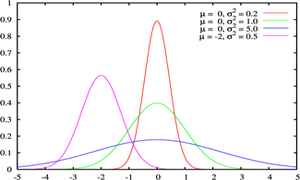 |
توزیع نرمال ، یکی از مهمترین توزیع ها در نظریه احتمال است. و کاربردهای بسیاری در علمفیزیک و مهندسی دارد.این توزیع توسط کارل فریدریش گاوس در رابطه با کاربرد روش کمترین مربعات در آمارگیری کشف شد.فرمول آن بر حسب ،دو پارامتر امید ریاضی و واریانس بیان میشود. همچنین تابع توزیع نرمال یا گاوس از مهمترین توابعی است که در مباحث آمار و احتمالات مورد بررسی قرار می گیرد چرا که به تجربه ثابت شده است که در دنیای اطراف ما توزیع بسیاری ازمتغیرهای طبیعی از همین تابع پیروی می کنند.
منحنی توزیع
منحنی رفتار این تابع تا حد زیادی شبیه به زنگ های کلیسا می باشد و به همین دلیل به آن Bell Shaped هم گفته میشود. با وجود اینکه ممکن است ارتفاع و نحوه انحنای انواع مختلف اینمنحنی یکسان نباشد اما همه آنها یک ویژگی یکسان دارند و آن مساحت واحد می باشد.
ارتفاع این منحنی با مقادیر میانگین (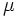 ) و انحراف معیار(
) و انحراف معیار( ) ارتباط دارد. با وجود فرمول نسبتا” پیچیده و دخیل بودن پارامترهای ثابتی چون عدد (p) یا عدد (e) در این فرمول، می توان از آن برای مدل کردن رفتار میزان IQ، قد یا وزن انسان، پراکندگی ستارگان در فضا و … استفاده کرد.
) ارتباط دارد. با وجود فرمول نسبتا” پیچیده و دخیل بودن پارامترهای ثابتی چون عدد (p) یا عدد (e) در این فرمول، می توان از آن برای مدل کردن رفتار میزان IQ، قد یا وزن انسان، پراکندگی ستارگان در فضا و … استفاده کرد.
 |
مقدار میانگین و واریانس |
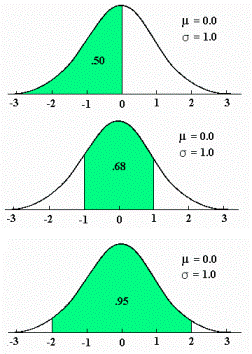
این منحنی دارای خواص بسیار جالبی است از آن جمله که نسبت به محور عمودی متقارن می باشد، نیمی از مساحت زیر منحنی بالای مقدار متوسط و نیمه دیگر در پایین مقدار متوسط قرار دارد و اینکه هرچه از طرفین به مرکز مختصات نزدیک می شویم احتمال وقوع بیشتر می شود.
سطح زیر منحنی نرمال برای مقادیر متفاوت مقدار میانگین و واریانس فراگیری این رفتار آنقدر زیاد است که دانشمندان اغلب برای مدل کردن متغیرهای تصادفی که با رفتار آنها آشنایی ندارند، از این تابع استفاده می کنند. بعنوان یک مثال در یک امتحان درسی نمرات دانش آموزان اغلب اطراف میانگین بیشتر می باشد و هر چه به سمت نمرات بالا یا پایین پیش برویم تعداد افرادی که این نمرات را گرفته اند کمتر می شود. این رفتار را بسهولت می توان با یک توزیع نرمال مدل کرد.
تابع چگالی احتمال
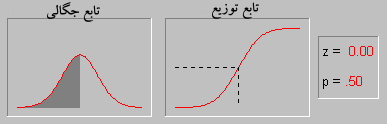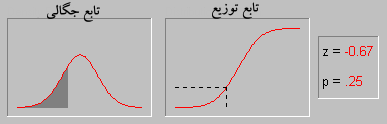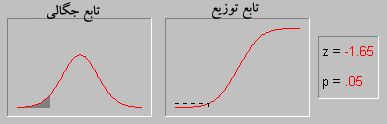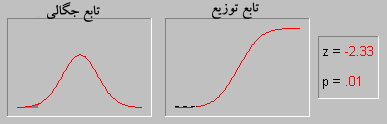
تابع چگالی احتمال برای توزیع نرمال بر حسب امید ریاضی و واریانس تعریف میشود.و تابع آن به صورت زیر است:

اگر در این فرمول 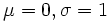 باشد در این صورت به آن تابع توزیع نرمال استاندارد گویند. در این حالت تابع توزیع به صورت زیر خواهد بود:
باشد در این صورت به آن تابع توزیع نرمال استاندارد گویند. در این حالت تابع توزیع به صورت زیر خواهد بود:

کاربردها
از مهمترین کاربردهای این تابع توزیع در دانش اقتصاد و مدیریت امروز می توان به مدل کردن پورتفولیوها (Portfolios) در سرمایه گذاری و مدیریت منابع نام برد. هنگامی که مقدار منفی برای متغییر معنی نداشته باشد معمولا” در محور x منحنی را منقل می کنند و مقدار میانگین – که دارای بیشترین احتمال وقوع هست – را به سمت مقادیر بزگتر شیفت میدهند.
 |
مرجع : مجله رشد