بخشی از یرگه سوالات امتحان پایان ترم خانم دکتر امین غفاری
( تقریبا هیچ تناسبی با درس ها و تمرین های داده شده نداشت )
۲ فصل آخر کتاب دکتر بهبودیان
تصمیم روا و پیرسان
و الگوریتم های یادگیری فضاهای برداری وهیلبرت در امتحان پایان ترم می آید
فضای برداری : مجموعه نا تهی است که نسبت به جمع و ضرب
اسکالر بسته است
هر عدد آلفا یی از C یا R انتخاب کنیم
فضای برداری یا خطی
پس فضای n یک فضای برداری می سازد
عملگر مشتق در فضای برداری یک عملگر خطی است
———————————–
ترکیب خطی :
یک ترکیب خطی از بردار ها انتخاب می کنیم ci*fi
استقلال خطی :
اگر هر ترکیب خطی ازشون بسازیم که حاصلش صفر نشود
f1 تا fn پایه ای برای V هستند.
فضای چند جمله ای هم یک فضای برداری است
————————————————
مفهوم متر
در فضایی که داریم یک معیار اندازه گیری به اسم متر تعریف می کنیم
X*X که یک تابع نا منفی است
فضای متری : مثل متر اقلیدسی (فاصله دو نقطه در فضای دو بعدی )
در عدد حقیقی
مفهوم کامل بودن یک فضا :
یک دنباله را میگوییم کوشی است اگر از یک جایی به بعد خیلی نزدیک
به هم شود
یک فضا را می گوییم کامل است اگر حد کوشی داخلش باشد
مفهوم d = distance که متر هست تعریف کردیم
مفهمو نرم : در فضای برداری
نورم یک تبدیل است در فضای برداری که به اعداد حقیقی نسبت داده
می شود.
نورم مفهوم اندازه داره
فاصله بین دو چیز است
قدر مطلق الفا
—————————————————–
فضای باناخ
فضای باناخ : یک نوع خاصی از فضاهای برداری
فضایی است که نورم دارد و نسبت به این نورم کامل است
—————————————————–
مفهوم Dot Product
ضرب داخلی یک نگاشت است
که خطی هست
فضای هیلبرت یک فضای باناخ است ولی ضرب داخلی
یک ماتریس را می توان به دید
ترانهاده ماتریس
ماتریس متعامد (تک تک سطر هاش دو به دو نسبت به هم عمودمد )
اگر ضرب داخلی دو بردار صفر شود آنگاه آن دو بردار نسبت به هم عمودند
یک مجموعه مستقل خطی می سازند
کل تعداد سطر ها
رتبه ماتریس با درجه ماتریس برابر است
Full Rank است
——————————————————–
مفاهیم جبر خطی بسیار پر کاربرد هست
ماتریس معین مثبت ، مقادیر ویژه اش حتما مثبت است
تعریف نورم القایی
اگر ماتریس مربعی باشد …
[U Lambda O]=svd(M)
Lambda in Matlab, is a m*n matrix whose first n rows and all columns, construct a diagonal matrix having lambdas an the diagonal.
۹۱/۰۲/۰۷ ESL
فرض میکنیم 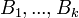 یک افراز برای فضای نمونه ای
یک افراز برای فضای نمونه ای  تشکیل دهند. طوری که به ازای هر
تشکیل دهند. طوری که به ازای هر 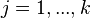 ، داشته باشیم
، داشته باشیم 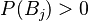 و فرض کنید
و فرض کنید  پیشامدی با فرض
پیشامدی با فرض  باشد، در اینصورت به ازای
باشد، در اینصورت به ازای 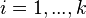 ، داریم:
، داریم:

تصمیم بیز : تصمیمی است که ریسک بیز آن کمترین باشد
تابع ریسک بیز
ریسک پسین
چگالی پیشین اطلاعاتی که از قبل داریم
چگالی پسین ، احتمال شرطی به شرط تتا
اگر تصمیم بیز داشته باشیم
ریسک پسین کمترین مقدار خودش را دارد
اگر تابع زیان درجه ۲ باشد می نیمم بیز E(teta|x) است
E(L(teta , d)
در آمار، توزیع احتمال پیشین یک کمیت احتمالاتی مانند  (که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد.
(که مثلاً میزان رای به یک نامزد انتخابات را مدل می کند.) یک توزیع احتمالاتی است که میزان عدم قطعیت یک فرد را در مورد آن کمیت قبل از مشاهده داده نشان می دهد.
کمیت احتمالاتی می تواند پارامتر یا متغیر نهان باشد.
با استفاده از قضیه بیز میتوان احتمال پیشین را در درستنمایی داده مشاهدهشده ضرب و پس از نرمالیزه کردن توزیع احتمال پسین را بهدست آورد.
احتمال پیشین کاملاً به نظر متخصص داده و آگاهی قبلی او در مورد داده بستگی دارد.
در آمار بیزی، توزیع احتمال پسین یک کمیت احتمالاتی توزیع احتمالی است پس از مشاهده شواهد (داده ). به عبارت دیگر، توزیع احتمال پسین احتمال شرطی آن کمیت است به شرط دیدن داده.
به بیان ریاضی: احتمال پسین یک پارامتر  پس از مشاهده داده
پس از مشاهده داده  برابر است با
برابر است با 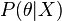 . اگر
. اگر 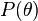 احتمال پیشین
احتمال پیشین  ، یعنی آگاهی پیشین ما در مورد
، یعنی آگاهی پیشین ما در مورد  ، را نشان دهد، با استفاده از قاعده بیز میتوان نوشت:
، را نشان دهد، با استفاده از قاعده بیز میتوان نوشت:
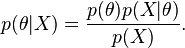
که در آن  درستنمایی داده را نشان میدهد. برای به خاطر سپردن این رابطه میتوان به صورت زیر نیز فکر کرد:
درستنمایی داده را نشان میدهد. برای به خاطر سپردن این رابطه میتوان به صورت زیر نیز فکر کرد:

برای امتحان ۱ خرداد فصل ۳ ( رگرسیون subset selection , Ridge , Lasso , PCR) و تصمیم آماری تا ابتدای تصمیم روا ( ابتدای فصل ۶ گرفته می شود.
فصل ۶ و ۷ برای پایان ترم امتحان گرفته می شود
کتاب تصمیم آماری دکتر بهبودیان را بگیرید
شماره تلفن کتابفروشی که دوستان در اختیار گذاشتند :
۶۶۴۰۵۴۰۳
۶۶۴۷۵۷۹۴
منبع : ویکی پدیا
قضیه بیز :
http://fa.wikipedia.org/wiki/%D9%82%D8%B6%DB%8C%D9%87_%D8%A8%DB%8C%D8%B2
احتمال پیشین :
http://fa.wikipedia.org/wiki/%D8%A7%D8%AD%D8%AA%D9%85%D8%A7%D9%84_%D9%BE%DB%8C%D8%B4%DB%8C%D9%86
احتمال پسین :
http://fa.wikipedia.org/wiki/%D8%A7%D8%AD%D8%AA%D9%85%D8%A7%D9%84_%D9%BE%D8%B3%DB%8C%D9%86
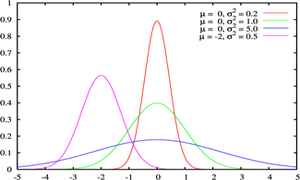 |
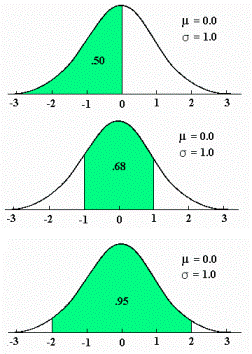
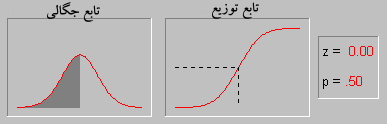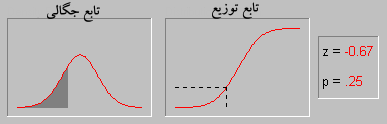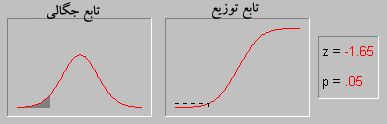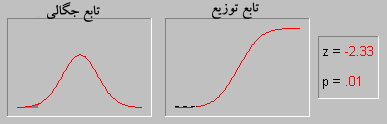
توزیع نرمال ، یکی از مهمترین توزیع ها در نظریه احتمال است. و کاربردهای بسیاری در علمفیزیک و مهندسی دارد.این توزیع توسط کارل فریدریش گاوس در رابطه با کاربرد روش کمترین مربعات در آمارگیری کشف شد.فرمول آن بر حسب ،دو پارامتر امید ریاضی و واریانس بیان میشود. همچنین تابع توزیع نرمال یا گاوس از مهمترین توابعی است که در مباحث آمار و احتمالات مورد بررسی قرار می گیرد چرا که به تجربه ثابت شده است که در دنیای اطراف ما توزیع بسیاری ازمتغیرهای طبیعی از همین تابع پیروی می کنند.
منحنی رفتار این تابع تا حد زیادی شبیه به زنگ های کلیسا می باشد و به همین دلیل به آن Bell Shaped هم گفته میشود. با وجود اینکه ممکن است ارتفاع و نحوه انحنای انواع مختلف اینمنحنی یکسان نباشد اما همه آنها یک ویژگی یکسان دارند و آن مساحت واحد می باشد.
ارتفاع این منحنی با مقادیر میانگین (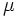 ) و انحراف معیار(
) و انحراف معیار( ) ارتباط دارد. با وجود فرمول نسبتا” پیچیده و دخیل بودن پارامترهای ثابتی چون عدد (p) یا عدد (e) در این فرمول، می توان از آن برای مدل کردن رفتار میزان IQ، قد یا وزن انسان، پراکندگی ستارگان در فضا و … استفاده کرد.
) ارتباط دارد. با وجود فرمول نسبتا” پیچیده و دخیل بودن پارامترهای ثابتی چون عدد (p) یا عدد (e) در این فرمول، می توان از آن برای مدل کردن رفتار میزان IQ، قد یا وزن انسان، پراکندگی ستارگان در فضا و … استفاده کرد.
 |
مقدار میانگین و واریانس |
این منحنی دارای خواص بسیار جالبی است از آن جمله که نسبت به محور عمودی متقارن می باشد، نیمی از مساحت زیر منحنی بالای مقدار متوسط و نیمه دیگر در پایین مقدار متوسط قرار دارد و اینکه هرچه از طرفین به مرکز مختصات نزدیک می شویم احتمال وقوع بیشتر می شود.
سطح زیر منحنی نرمال برای مقادیر متفاوت مقدار میانگین و واریانس فراگیری این رفتار آنقدر زیاد است که دانشمندان اغلب برای مدل کردن متغیرهای تصادفی که با رفتار آنها آشنایی ندارند، از این تابع استفاده می کنند. بعنوان یک مثال در یک امتحان درسی نمرات دانش آموزان اغلب اطراف میانگین بیشتر می باشد و هر چه به سمت نمرات بالا یا پایین پیش برویم تعداد افرادی که این نمرات را گرفته اند کمتر می شود. این رفتار را بسهولت می توان با یک توزیع نرمال مدل کرد.
تابع چگالی احتمال برای توزیع نرمال بر حسب امید ریاضی و واریانس تعریف میشود.و تابع آن به صورت زیر است:

اگر در این فرمول  باشد در این صورت به آن تابع توزیع نرمال استاندارد گویند. در این حالت تابع توزیع به صورت زیر خواهد بود:
باشد در این صورت به آن تابع توزیع نرمال استاندارد گویند. در این حالت تابع توزیع به صورت زیر خواهد بود:

از مهمترین کاربردهای این تابع توزیع در دانش اقتصاد و مدیریت امروز می توان به مدل کردن پورتفولیوها (Portfolios) در سرمایه گذاری و مدیریت منابع نام برد. هنگامی که مقدار منفی برای متغییر معنی نداشته باشد معمولا” در محور x منحنی را منقل می کنند و مقدار میانگین – که دارای بیشترین احتمال وقوع هست – را به سمت مقادیر بزگتر شیفت میدهند.
 |
مرجع : مجله رشد
۹۲/۱/۱۷ ESL
اگر سیگما را نداشته باشیم باید برآورد کنیم SSE
برآوردسیگما ۲ می شود SSEتقسیم بر درجه آزادی
امتحان از آمار و رگرسیون هست
بطور مستقیم از آمار امتحان نمی آید
مشابه نمونه سوالاتی که خانم گرجی حل می کنند
پروژه هم انجام بدهید در فصل ۳
۸ سری داده هست
۴ نمره اضافی پروژه دارد
مهلت تحویل پروژه تا زمانی که میشه نمره ها رو قطعی کرد( تیر یا مرداد)
بهتر است ۲ تا متغیر در نظر بگیرید
روشهای Shrinkage
اسلاید ۱۱ از ۱۹
Ridge Regression
توزیع Yi به شرط بتا j
سیگمای بتا j^2 ها را در نظر میگیریم
————————————
امروز مبحث Lasso Regression را توضیح میدهیم
مجموع مربعات خطا را مینیمم میکنیم به شرط اینکه سیگمای قدر مطلق بتا j ها از یک مقداری کمتر باشد
تفاوت ریج و لاسو :
در ریج هیچ ضریبی صفر نمی شود ولی در لاسو ممکن است ضرایب صفر شوند
در این ۳ روش پارامتر هایی دارند که باید آنها را مشخص میکنیم که به آن Cross Validation می گوییم
subset selection
df landa
می توانیم از تصویری از داده ها استفاده کنیم تا وضوح بهتری داشته باشیم
کاری که در Principal Component Regression انجام میدهیم تصویر سازی است
ماتریس مربع داریم که تجزیه میکنیم به دو ماتریس
ماتریس D (قطری) و ماتریس V ( اوتوگونال ) Di ها مقادیر ویژه هستند
اگر بتوانیم به این صورت بنویسیم از روش پرینسیپال به راحتی میتوانیم حل کنیم
Principal Component یعنی یک X داریم مولفه های اصلی اش را با تجزیه پیدا می کنیم
در واقع اگر دو بعد داشته باشیم p=2
یک سری داده داریم در قالب X1 , X2 که نقاط سبز را تشکیل می دهند
مولفه های اصلی D1 , D2 را پیدا کنیم
در این شکل نقطه ها در جهت D1 پراکنده شده اند
اگر بخواهیم متغیری را حذف کنیم بعد D2 را حذف می کنیم چون D1 مهم تر است
(اجباری هم در حذف بعد نیست )
مقادیر وِیژه را در متلب می توانیم با دستور (SVD(x’x محاسبه کنیم
به جای اینکه p تا Z داشته باشیم M تا Z را نگه میدارم
پس در Principal به جای اینکه بین x , z رگرسیون بگیرم بین y , z رگرس میکنم
M=p least Square
z=xv
کاهش بعد هم انجام داده می شود
۴ روش در این فصل گفتیم :
معمولا روش ریج دقیق تر است
امتحان از فصل ۱ و ۳ هست
۹۱/۱۲/۲۶
ریاضیات یادگیری
چهار شنبه ۹۲/۳/۴ کلاس حضوری امتحان از رگرسیون میان ترم گرفته می شود
آزمون فرض – فاصله اطمینان بایستی به صورت پیش فرض بدونید
رگرسیون چند گانه :
حالتی که p تا x داریم
x ها میتونن تبدیلی از بقیه x ها باشند
نا اریب هست
یک کمیت داریم MSE که یک جور ریسک هست ( امید تابع زیان )
Too many Predictors
۱- روش subset selection زیر مجموعه ای از متغیر ها را انتخاب میکنیم
۲- Cross Validation
۳- روش Shrinkage Methods ضرایب (Beta) را کوچک می کنیم به سمت صفر
بهتر است که نا اریب باشد.
نا اریب باشد یعنی خطا کم باشد ، واریانس کم باشد، امیدش با خودش برابر باشد.
همه x ها را در مدل می گذاریم ولی یک ضریب براشون می گذاریم
یکی از روش های شرینکیج Ridge Regression است
روش انقباظی
مجموع مربعات خطا می نیمم می کنیم با شرط اینکه جریمه در نظر میگیریم
از روش لاگرانژ
مزیت های Ridge :
مجموع توان ۲ پارامترها خیلی بزرگ نمی شود
لاندا را می توان با استفاده از روش Cross Validation محاسبه می کنیم و باید داده ها را باید استاندارد کنیم
رگرسیون لاسو هم مانند رگرسون ریج هست با این تفاوت که سیگمای بتا j ها به توان ۲ کمتر از S
سیگمای قدر مطلق بتا ها را در نظر می گیریم کمتر از S
رگرسیون لاسو تکنیک جدیدی است ولی ریج خیلی قدیمی است
۹۱/۱۲/۲۲
آزمون فرض
مثال :
میزان کارکرد کارمندان
نباید بی دلیل رد کنیم ، بنابراین از آزمون فرض استفاده می کنیم
یک فرض H0 داریم به صورت تساوی
Ha به صورت نامساوی (آزمون دوطرفه )
برای اینکه فرض H0 را بی دلیل رد نکنیم
مقادیری که خیلی به ندرت اتفاق می افتند ، به این مقادیر ناحیه
بحرانی گوییم
پس مراحل آزمون فرض
H0
Ha آلفا
n تعداد اعضای نمونه
انتخاب test
از آزمون Z در صورتی که میانگین جامعه معلوم باشد
در صورتی که میانگین جامعه معلوم نباشد از آزمون T استفاده می کنیم
مقادیر بحرانی را از جدول بدست می آوریم
————————-
Confidence Intervals VS Hypotheses Test
آزمون فرض VS فاصله اطمینان
دو نوع خطا داریم :
۱- فرض H0 را به ناحق رد کنیم ( خیلی بد است ) و باید الفا را کوچک
بگیریم
۲- فرض H0 نادرست باشد و رد نکنیم
در بعضی مسایل که آلفا را نداریم ، از p-value استفاده میکنیم
که احتمال رد فرض H0 به نا حق هست
—————————————–
Linear Space ( Vector Space )
فضا های برداری – ( فضا های خطی )
خیلی مهم است
یک مجموعه ای نا تهی از یک سری اعضا است
ویژگی های فضا های خطی :
نسبت به عمل جمع و ضرب بسته هست
۸ اصل جمع و ضرب
۱- خاصیت شرکت پذیری جمع
۲- خاصیت جابجایی جمع
۳- عضو خنثی جمع
۴- وجود عضو قرینه
۵- توزیع پذیری جمع نسبت به ضرب
۶- توزیع پذیری ضرب نسبت به جمع
۷- شرکت پذیری ضرب
۸- عضو خنثی ضرب
Linear Combination
ترکیب خطی
اگر c1 , c2 , …, cn هایی را پیدا کنیم که در بردار ضرب شود
ترکیب خطی می گوییم
میتونه یک ماتریس ترکیب خطی از ۲ ماتریس دیگه باشه
زیر فضای برداری
W زیر فضای برداری V هست به شرطی که زیر مجموعه V باشد
و W باید خواص بردار V را داشته باشد
عضو خنثی V را داشته باشد
مفهومspan مولد linear independence ،basis پایه ، cooridates مولفه
هر عضوی از V مثل f بتوانیم عدد c1 jتا cn داشته باشیم که
f=c1.f1+c2.f2+…+cn.fn
مستقل خطی :
بردار های f1 تا fn مستقل خطی هستند اگر به ازای c1f1+c2f2+…
+cnfn=0 باشد.
ترکیب خطی آنها صفر باشد
پایه :
اگر f1 تا fn بردار V را تولید کنند
مولفه :
(c1-d1).f1+…+(cn-dn).fn=0
b1.f1.+…+bn.fn=0
ci=dn
c1 تا cn مولفه نسبت به پایه f1 تا fn می گوییم
بعد ( Dimention (
تعداد اعضای f ها n تا که باشد
dim(V)=n
n بعد فضای برداری V هست
تعریف Finite فضا های برداری متناهی :
اگر فضای برداری پایه های متناهی داشته باشد فضای متناهی می
گوییم
تابع هموار : از تابع هر چقدر که مشتق بگیریم باز هم مشتق پذیر باشد
سوال : یک پایه برای فضای چند جمله ای های حداکثر از درجه n
مثل : x^4-1
۹۱/۱۲/۱۹
وقتی میگوییم رگرسیون خطی نسبت به بتا هست
پس در رگرسیون چند گانه خطی
صفحه ۴ از ۱۹
RSS بتا رو میشه به فرم ماتریسی نوشت
اگر y رو نسبت به x ها رسم کنیم میبینیم که
اگر از این رابطه نسبت به x مشتق بگیریم
فرضمان این است که توزیعشن نرمال هست
برآورد گری که بدست آوردیم یک برآورد گر خوب است ( نا اریب )
واریانسش هم کم هست
یک ترکیب خطی از تتا را بدست می اوریم
چون بتا هت را نداریم پس تتا هت هم مجهول است
۱۳۹۱/۱۲/۰۸
فاصله اطمینان برای نسبت جامعه
در یک جامعه دانشگاهی ( قبول شدگان و رد شدگان ) می خواهیم فاصله
اطمینان را بدست بیاوریم
آزمایش دو جمله ای برای n-1 داریم
فاصله اطمینان که برای p می خواهیم بدهیم
رگرسیون
یک سری ورودی داریم
یک سری خروجی داریم
در رگرسیون دنبال رابطه خطی بین ورودی ها و خروجی ها هستیم
ضرایب رگرسیون را تشخیص بدیم
مدل چیست ؟
چند نوع مدل داریم ؟
مدل : نمایش دهنده بعضی پدیده ها هست
مدل تعیینی : به صورت دقیق ریاضی هست ( مثل : نیرو = شتاب * جرم )
مدل احتمالی : بعضی قسمت های مدل احتمالی تعیینی است + درصدی خطا
که ممکن است این خطا ناشی از اندازه گیری باشد
مدل رگرسیونی : یعنی خطای تصادفی در مساله داریم
مدل رگرسونی که پیدا میکنیم رابطه بین متغیر ها
متغیر های وابسته dependent ( متغیر های پاسخ )(متغیر output)
متغیری است که باید پیش بینی کنیم
مثال : تاثیر تبلیغ در فروش
کاربرد آن برای پیشبینی ( estimation ) است
باید متغیر های مساله را مشخص کنیم
ابتدا فرض میکنیم که رابطه خطی است
انواع رگرسیون :
۱- رگرسیون ساده ( یک متغیر وابسته – یک متغیر مستقل )
۱-۱ رگرسیون ساده خطی
۱-۲ رگرسیون ساده غیر خطی
۲- رگرسیون چند گانه ( بیش از ۲ متغیر مستقل داشته باشیم
صفحه ۲۸ فرمول
در مدل تعیینی
Y(i)=B(0)+B(1)X(i)+e(i)
e خطای تصادفی
X = رگرسور Input
Y = output
۰ beta = عرض از مبدا
beta 1 شیب خط
صفحه ۳۴
در نمونه آماری ما نقطه هایی را در نظر میگیرم و خط را تخمین میزنیم
e(i) خطای
معادله خط را بر آورد کردیم
خطی را که پیدا میکنیم باشد اپسیلون های کمتری داشته باشد
بهترن برازش (خط ) را باید پیدا کنیم
برازشی بهتر است که فاصله بین y و y^ کمترین باشد
خطی خوب است که مجموع مربعات خطا کمترین باشد List Square minimun (SSE)
اگر هیچ هزینه ای برای تبلیغ نکنیم میزان فروش -۰٫۱ می شود
با نرم افزار متلب انجام میدیم
X بار یعنی میانگین
Download PDF : The Elements of Statistical Learning