خلاصه درس خوشه بندی – دکتر زارع – ۹۲/۰۹/۱۸

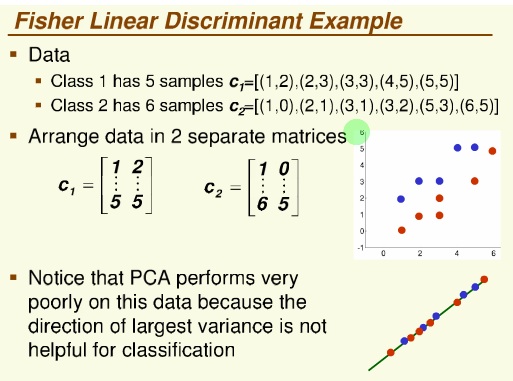
روش فیشر

پراکنش داده ها
داده ها را از دو بعد به یک بعئ می خواهیم map کنیم

فقط جهت بردار مهم است
معیار یا جهت مناسب ، جهتی است که جدا پذیری دو کلاس زیادباشد
و تقسیم بر پراکنش درون کلاسی هم می کنیم (که هر چه کمتر باشد بهتر است )

نام این مساله : مساله مقدار ویژه تعمیم یافته

این نمونه معمولا در امتحان می آید
یا مفهوم این که Fisher با PCA جه فرقی می کند

نمونه ای که ممکن است در امتحان بیاید

معمولا دوستان در اینورس کردن ماتریس اشتباه می کنند
جهتش هم می خواهیم که رسم کنید
——————————–

روش های خوشه بندی

فرض می کنیم دستگاهی برای دسته بندی و بسته بندی ماهی داریم
برای تفکیک ماهی ها از روش های خوشه بندی می خواهیم استفاده کنیم

اولین قدم data Gathering هست – طبقه بندی اطلاعات اولیه جمع آوری شده

خیلی از مسایل خوشه بندی تعبیر Geo metric دارند
اگر بتوانیم Rule برایش تعریف کنیم

آقای فیشر اولین بار مساله pattern Recognition را حل کرد و داده های IRIS رو مطرح کرد

قانون که می گذاریم باید برای داده های بعدی هم خوب کار کند
هر چه مدل ساده تر باشد احتمال اینکه برای داده های بعدی هم کار کند محتمل تر است

over fitting
به صورت simple از هم جدا کنیم

Predictive Accuracy
صحت پیش بینی
Accuracy صحت : تعداد صحیح ها تقسیم بر تعداد کل نمونه ها
خطا : تعداد اشتباهات تقسیم بر تعداد کل نمونه ها

روش k-fold :

داده ها را به دو قسمت تقسیم می کنیم
داده های train و داده های test
یک مدل را بر اساس داده های Train می سازیم و test را با آن آزمایش می کنیم
داده ها را به k قسمت مساوی تقسیم می کنیم
قدم اول : مدل را می سازم و با قسمت k ام خطای مدل را بدست می آوریم
قدم دوم : k-1 را Train در نظر می گیریم و باز خطا را بدست می آوریم

یک مقاله به صورت تجربی (imperical ) بخش ها را به ۱۰ قسمت تقسیم کردند
و ما هم اکثر مسایل رو ۱۰-fold می گوییم
Nearest Neighbor Classifier
هر داده جدیدی که آمد فاصله اش را با کل داده های قبلی حساب کن ، سپس sort کن

کمترین فاصله ها اکثریت را پیدا می کنیم
جزء روش های Lazy محسوب می شود چون خیلی هزینه بر هست ( با محاسباتی زیاد
هست )

جلسه بعد nearest neghbor را می گوییم