نکاتی درباره متلب

نکاتی درباره کار با نرم افزار متلب

روش اول تعریف کردن بردارها

» v=[1 2 3]

v =

۱ ۲ ۳

» w=[‘abcd’ ‘1234’]

w =

abcd1234

• برای تعریف بردارهای عددی حتما” باید از کروشه استفاده کرد ولی استفاده از آنها برای متغیرهای حرفی الزامی نیست.

•  حالت خاصی از بردار عبارتست از بردار تهی که به صورت [ ] تعریف می گردد.

روش دوم تعریف کردن بردارها

» x = 0:4

 x=

۰ ۱ ۲ ۳ ۴

» x = (0:0.2:1)

x =

۰  ۰٫۲  ۰٫۴  ۰٫۶  ۰٫۸  ۱

عملیات ماتریسی روی آرایه ها

در MATLAB می توان دو نوع عملیات روی آرایه‌ها انجام داد که به آنها عملیات ماتریسی و عملیات عضو به عضو می گویند.

عملیات ماتریسی شامل محاسبه ترانهاده، ضرب ماتریسی، جمع و تفریق آرایه های هم اندازه و غیره می شود.

» m=[1 2 3

۴ ۵ ۶];

» ۲*m

ans =

۲ ۴ ۶

۸ ۱۰ ۱۴

یا

» m+1

ans =

۲ ۳ ۴

۵ ۶ ۸

» r=rand(2,4)

r =

۰٫۹۵۰۱ ۰٫۶۰۶۸ ۰٫۸۹۱۳ ۰٫۴۵۶۵

۰٫۲۳۱۱ ۰٫۴۸۶۰ ۰٫۷۶۲۱ ۰٫۰۱۸۵

» r’

ans =

۰٫۹۵۰۱ ۰٫۲۳۱۱

۰٫۶۰۶۸ ۰٫۴۸۶۰

۰٫۸۹۱۳ ۰٫۷۶۲۱

۰٫۴۵۶۵ ۰٫۰۱۸۵

» r=rand(2,4);

» v=[1:4];

» r*v’

ans =

۶٫۶۶۳۶

۳٫۵۶۳۴

چندجمله‌ای‌ها

یک چند جمله‌ای در MATLAB به صورت یک بردار سطری که مولفه های آن ضرایب چندجمله ای به ترتیب نزولی هستند معرفی می شود.

این نرم افزار قابلیت محاسبه‌ی ریشه های یک چند جمله ای، محاسبه مقدار یک چند جمله ای، ضرب و تقسیم چند جمله ایها، مشتق چند جمله ای و نیز منحنی رگرسیون چند جمله ای را محاسبه نماید.

تعریف چندجمله‌ای‌ها:

مثال: برای تعریف چندجمله ای

p(x) = x٣ -٢x +5

» p=[1 0 -2 5];

ریشه های یک چند جمله ای:

ریشه های یک چند جمله ای را می توانید به صورت زیر بدست آورد:

» r=roots(p)

r =

-۲٫۰۹۴۶

۱٫۰۴۷۳ + ۱٫۱۳۵۹i

۱٫۰۴۷۳ – ۱٫۱۳۵۹i

تابع polyval  مقدار چند جمله ای را در هر نقطه محاسبه می‌نماید. برای مثال مقدار ( ۵p( به طریق زیر محاسبه می گردد:

 » polyval(p,5)

ans =

۱۲۰

ضرب و تقسیم چند جمله ایها

برای ضرب و تقسیم چند جمله ایها می توانید توابع conv و deconv را بکار ببرید.

» a=[1 1 1]; b=[1 -1];

» c=conv(a,b)

c =

۱ ۰ ۰ -۱

مشتق چند جمله ای

مشتق چند جمله ای را می توانید با بکار بردن تابع polyder محاسبه کرد:

» c=polyder(a)

c =

۲  ۱

رگرسیون منحنی چند جمله ای

تابعpolyfit ضرایب بهترین چند جمله ای را پیدا می کند که از میان مجموعه نقاط داده شده عبور می نماید.

» x=[1 2 3 4 5];

» y=[5.5 43.1 128 290.7 498.4];

» p=polyfit(x,y,3)

p =

-۰٫۱۹۱۷ ۳۱٫۵۸۲۱ -۶۰٫۳۲۶۲ ۳۵٫۳۴۰۰

عدد ۳ در تابع نشانگر درجه منحنی رگرسیون است.

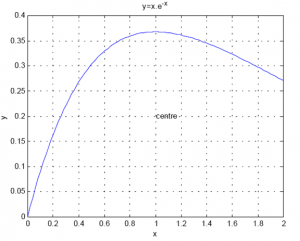
رسم نمودار

 » x=linspace(0,2); y=x.*exp(-x);

» plot(x,y)

» grid

» xlabel(‘x’)

» ylabel(‘y’)

» title(‘y=x.e^{-x}’)

» text(1,.2,’centre’)

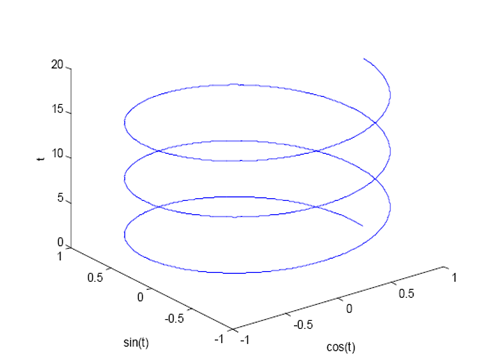
دستورهای زیادی در MATLAB برای ترسیم نمودارهای سه بعدی وجود دارند. یک منحنی سه بعدی را می توانید به کمک دستور  Plot3رسم کنید:

» t=0:.01:6*pi;

» plot3(cos(t),sin(t),t)

» xlabel(‘cos(t)’)

» ylabel(‘sin(t)’)

» zlabel(‘t’)

(m-files) برنامه نویسی

m-file ها می توانند به دو شکل برنامه اصلی و تابع باشند. برنامه اصلی عبارتست از مجموعه ای از دستورها که می توان آنها را بطور جداگانه در محیط کارMATLAB اجرا نمود. هنگامی که نام برنامه اصلی را در محیط کار MATLAB بنویسیم این دستورها به ترتیب اجرا می گردند. به عنوان مثال برای محاسبه حجم گاز کامل، در دماهای مختلف و فشار معلوم، دستورات زیر را در ویرایشگر MATLAB نوشته و سپس تحت عنوان pvt.m ذخیره می‌کنیم:

% A sample scritp file: pvt.m

disp(‘ Calculating the volume of an ideal gas.’)

R = 8314; % Gas constant (J/kmol.K)

t = …

input(‘ Vector of temperature (K) = ‘);

p = input(‘ Pressure (bar) = ‘)*1e5;

v = R*t/p; % Ideal gas law

% Plotting the results

plot(t,v)

xlabel(‘T (K)’)

ylabel(‘V (m^3/kmol)’)

title(‘Ideal gas volume vs temperature’)