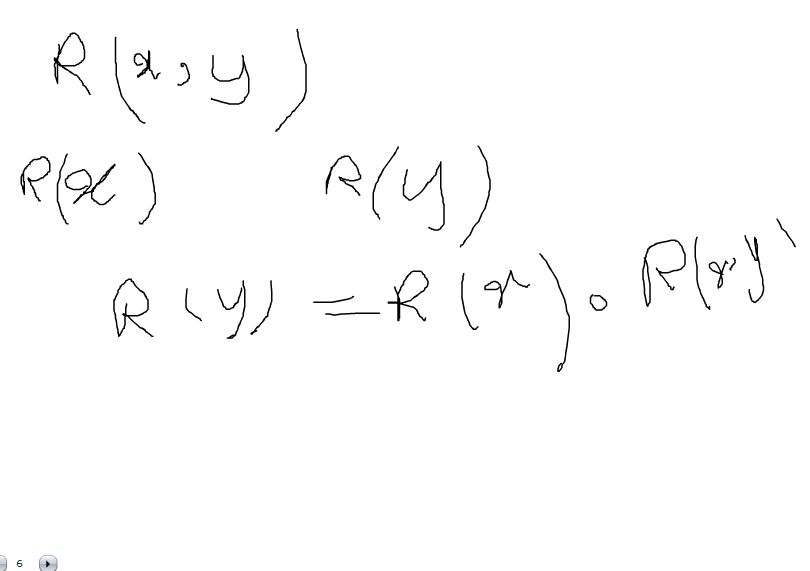خلاصه درس مبانی محاسبات نرم ۹۳/۰۲/۰۶
زیر ساخت مورد نیاز برای ترکیب قوانین مختلف فازی
اسلاید ۲۴
Inference Methods
دو تا قانون بر اساس منطق فازی ، فرض و حکم را داریم
برای هر یک از قوانین درجه تحریک ( ارضا شدن ) آن قانون را بدست
بیاوریم
در روش ممدانی : برای اینکه یک استدلال فازی را صورت بدهیم از اپراتور
مینی مم فازی که ترکیبی هست که در قالب max min مطرح می شود
قابل تعمیم روی قوانین مختلف فازی هست
اسلاید ۲۵
…
هر تعداد قانون که داشته باشیم با عملگر مینیمم یکپارچه می کنیم و آلفا
آی را محاسبه می کنیم و مینیمم می گیریم
U0 و V0 را می دهند
قانون اول : بین عضویت U0 در A1 و عضویت V0 در B1مینیمم را
محاسبه می کنیم که آلفا می نامیم
طبق روش ممدانی : از بین ذوزنقه سفید و مشکی ماکزیمم را در نظر می
گیرد
اسلاید ۲۷ :
اگر سناریو ها بجای دو عدد حقیقی دو مجموعه فازی باشد کمی مساله
پیچیده تر می شود
اسلاید ۲۸ :
دو عدد فازی به ازای هر قانون داریم
‘A و’B هم دو سناریوی فازی داریم
پس در دو حالت ممدانی ( وروی کریسپ و فازی ) با ترکیب کردن
maximum similarity
اسلاید ۲۹ :
مثال عددی :
A(0,2,4)
B(3,4,5)
در تک سناریوی U0=3
محاسبه می کنیم که A را در چه نقطه ای قطع میکند
اسلاید ۳۰ :
مثال ( ورودی فازی )
نقاط تقاطع ۲/۳ هست گه ذوزنقه جدید بدست می آوریم
اسلاید ۳۱ :
در لارسن هر جاکه minimum داریم Productرا جایگزین می کنیم
اجتماع بین قانون یکم تا قانون n ام باید داشته باشیم
اسلاید ۳۲ :
دو عدد فازی در نظر می گیریم
دو تا سناریوی U0 و V0 داریم
مینیمم عدد آلفا ۱ را به ما میدهد
در قانون اول مثل سفید را بدست می آووریم
و در قانون دوم مثلث سیاه رنگ را بدست می آوریم
مثال : سرعت ماشین زیاد بوده و جاده لغزنده بوده سپس ماشین تصادف
کرده (دراینجا دو عدد فازی داریم و یک حکم)
اثربخشی فازی بیشتر در جایی است که انسان منشا اثر هست
کثیف بودن لباس ( پارامتر فازی ) تعداد دور ماشین لباسشویی مورد نیاز
برای شستن لباس ها
اسلاید ۳۸ :
با ازای تک تک …. در حکم ها نگاه می کنیم درجه عضویت آلفا i مرتبط با
چه قسمتی است
اسلاید ۳۹ : دو تا قانون داشتیم فرضیات دو عدد … شکل هستند
بر خلاف روش ممدانی ولارسن که خروجی فازی بود ، در Tsukamato
خروجی به صورت عددی است
آخرین تکنیک : TSK
اگر سناروی U درمجموعه فازی A و سناریوی V در مجموعه فازی B
باشد
جمع بندی :
لارسن و ممدانی ، در ورودی های کریس پ و فازی خروجی مجموعه فازی
داشتند
حالت سوم : Tsulamato حکم مجموعه فازی با درجه عضویت یکنواخت
که خروجی به صورت عددی است
حالت آخر TSK : به صورت تابع حقیقی محور ازورودی های مساله
با استفاده از قوانین مینیمم گیری درجه عضویت سناریو ها را بدست می
آوریم