با سلام
تا ۲۵ بهمن فرصت دارید.
موفق باشید.
-- Hadi Zare, Ph.D Assistant Professor, Faculty of New Sciences and Technologies, University of Tehran, Iran
Feb 022014
Jan 082014
On Wednesday, January 8, 2014 12:19 AM, Hamid Kashani <clustering_1391@yahoo.com> wrote:
با سلام
مهلت تمرین آخر دوشنبه ۷ بهمن ۱۳۹۲ تمدید شد.
ضمنا تاریخ فوق هرگز قابل تمدید نمی باشد و هیچ تمرینی پس از آن قابل قبول نخواهد بود.
موفق باشید
برادران
Jan 012014
با سلام
لطفا در مورد فایلهای همراه این ایمیل در سایت باشگاه مجازی دانشگاه امیرکبیر اطلاع‌رسانی شود.
البته این فایلها در روی سایت درس نیز قرار خواهد گرفت.
در مورد درخواست برخی از دوستان در مورد سری نهایی تمرین‌ها، تمرین همان تمرین قبلی است،
و دوستان بایستی تنها دو صفحه گزارش بر اساس دستورالعملی که توسط آقای دکتر برادران تهیه شده است،
انجام دهند.
clustering project instructions
—
Hadi Zare, Ph.D
Assistant Professor,
Faculty of New Sciences and Technologies,
University of Tehran, Iran
Dec 162013
خلاصه جلسه جبرانی خوشه بندی ساعت ۵ تا ۶:۳۰ دکتر زارع ۹۲/۰۹/۲۵
Classification
فیشر :
با استفاده از توزیع گوسی روش فیشر را بدست آورد در بحث Pattern Recognition
داده ها را به دو دسته train و test تقسیم می کنیم
اگر بتوانیم یک جدا ساز ساده تعیین کنیم برای داده های تست عملکرد خوبی داشته باشیم
nearest Neighbor در صورت اضافه شدن داده جدید ،
یک پیش پردازش برای کاهش بعد انجام می دهیم
و معمولا از Feature Selection برای بیرون انداختن داده های نامربوط استفاده می کنیم
برای تشخیص پارامتر های موثر
از یکی از این سه روش می توانیم استفاده کنیم
-Forward Selection
– Backward Elimination
– Bi-Directional search
در بحث Distanse های مختلفی می توانیم استفاده کنیم ( اقلیدسی – منهتن – ماهالونوبیس )
دو تا اسم داریم Peter , Piotr
از اسم اول با ۳ عملگر می توانیم به اسم دوم برسیم
————————————
فایلهای زیر آپلود شد
Clustering Final exam
sharifi test
intro_SVM_new
classification – part 4
———————————-
———————————-
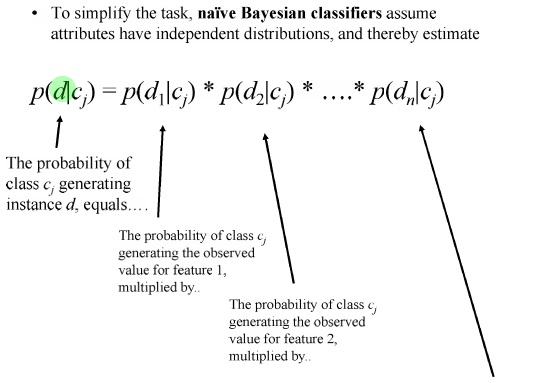
Naive Bayes رو معمولا بر اساس گراف می کشند
نایو بیز نسبت به Future های نامربوط حساس نیست
چون در واقع ویژگی ها از هم مستقلند اثر یک ویژگی از بین می رود
آیا می شود روش Naive Bayes را بهتر کرد ؟ بله
مزایا و معایب روش Naive Bayes:
————————————–
در امتحان نمی آید
SVM : Support Vector Machine
ماشین بردار پشتیبان
آقای vladimir vapnik مطرح کرد ۱۹۸۰
Statistical Learning Theory
Dataset – MNIC
error rate بسیار کمی داشت
اولین بار روش Kernel را با SVM مطرح کردند
اگر دو کلاس داشته باشیم و بتوانیم با یک خط جدا کنیم پس بی نهایت خط دیگر می توانیم رسم کنیم
بهترین خط را کدام در نظر بگیریم
دو خط مرزی را در نظر می گیریم و مرز تصمیم گیری را در میانگین این دو خط مرزی در نظر می گیریم
Margin را باید Maximize کنیم
KKT Conditions
سر امتحان
ماشین حساب بیارید
دندوگرام باید بکشید
K-means
GMM
PCA
Fisher
روشهای classification
Naive Bayes و K-nearest Neighbor را باید بلد باشد
h.zare@ut.ac.ir
مقاله ها را به این ایمیل بفرستید
تا ۱۵ بهمن تاریخ نحویل پروژه هست
Dec 142013
نوشته های تدریس یار درس خوشه بندی استاد حمیدرضا برادران کاشانی
دوستان عزیز لطفا همه توجه کنند و هیچ کامنتی نگذارند
۴ نوع تمرین است
هر کسی بایستی تمرین گروه خود را بصورت مستقل انجام دهد.
یعنی هرگز کار گروهی نیست
گروه ها را بصورت رندوم انتخاب کرده ایم.
تمرین در هر گروه بر اساس بهترین تمرین در آن گروه و بصورت نسبی ارزیابی می شود.
دوستان امروز صدا نداریم.
بنابراین گروه آسان یا سخت نداریم. یا تمرین آسان و سخت
اهمیت این تمرین که در واقع بصورت یک مینی پروژه است از سایر تمرین ها بیشتر بوده
بنابراین دوستانی که در تمرین های گذشته کارشان به نظرشان اشکالات یا کاستی های داشته می توانند در این مینی پروژه جبران نمایند.
باز هم تاکید می کنم که بهترین فردی که در هر گروه بهترین و کاملترین گزارش در آن
گروه را ارائه دهد معیاز ارزیابی آن گروه می باشد.
ضمنا تمرین فیشر را نیازی نیست کسی نجام دهد
این تمرین را به عنوان آخرین تمرین درس در نظر گرفته ایم.
لطفا تمرین را دانلود کنید همه چیز اعلام شده
پیاده سازی نمی خواهد فقط گزارش کامل
روش هایی که هدفشان تمایز بین داده های دو یا چند کلاس است مثل فیشر دیگر چه روش هایی داریم
در مورد تمرین سوالی نیست؟
روش VQ
, Kmeans
چه روش های مشابهی وجود دارند
در تمامی گروه ها هدف بیان توابع cost function جدید است
اسم تمرین در سایت shw2 است
دوستان اگر با تمرین کمی کار کنند
بعد می توانند سوالاتشات را از طریق ایمیل clustering_1391 – yahoo بپرسند
Dec 122013
پروژه ها را شروع کنید
تا آخر بهمن احتمالا وقت هست برای تحویل پروژه
جواب نمونه سوالات ترم گذشته
سوال ۱ :
a) درست است
b) نادرست است (تحلیل مولفه های اصلی نیست – اصلا به تعداد کلاسها توجهی ندارد )
c) نادرست ( EM در GMM بود و در سلسه مراتبی نیست )
d) درست است
e) درست است
f) اشتباه است
سوال ۲ :
a) در PCA مولفه های موثر در را مشخص می کند
b ) فیشر – خطی بودن
c) رسم نقاط – با روش فیشر حل می کنیم
SW^1(mu1-mu2)
سوال ۳ :
a) برچسب داشته باشد بهتر است
b) تعداد داده های اشتباه تقسیم بر تعداد کل مشاهدات
برای بهتر شدن و جلوگیری از Overfitting از CrossValidation میشه استفاده کرد
c) هزینه محاسباتی زیاد است – برای کاهش بعد
ابتدا باید similarity را باید حساب کنیم ( بجای محاسبه distance )
نمونه جدید را داریم
نونه سوال ترم پیش : نمونه سوال خوشه بندی – دکتر زارع
————-
ارائه خانم مهندس شیخیان
روش خوشه بندی Cure
یک روش خوشه بندی سلسله مراتبی است
سلسله مراتبی ها
خوشه ها از بالا به پایین خوشه ها مشخص تر هستند ولی انباشتگیشون بیشتر است
تمرکز خوشه بندی یک نقطه هست و بر اساس میانگین خوشه ها می تواند با هم merge شوند
مزیت Cure نسبت به سایر روشهای سلسله مراتبی تشخیص خوشه های کروی و غیر کروی را می تواند
انجام دهد
مزایای Cure حساس نبودن به شکل هست
وبه Outlier حساس نیستند چون خوشه بندی را بر اساس میانگین انجام می دهند و نه بر اساس فاصه
نقطه ها
یک الفا بین صف و یک تعریف می شود
و هر چه به صفر نزدیک تر باشد بر اساس تمام نقاط ورودی
و هر چه به یک نزدیک شود بر اساس یک نقطه انجام می دهد
در هر خوشه که تعدای نقاط را داریم
بر اساس Merge شدن نقاط هست
بقیه نقاط در مراحل بعدی با هم Merge می شوند
این روش ار random Sample استفاده می کند
خوشه بندی در دو مرحله صورت می گیرد
دیتا های ورودی پارتشین می شود
خوشه بندی ناقص انجام می شود
outlier های حذف می شود
خیلی مهم است که اندازه random Sample درست محاسبه شود.
چون ممکن است حجم محاسبات زیاد شود و یا اینکه خیلی داده ها دیده نشوند
شرط خاتمه این الگوریتم نسبت n به q هست
در سرعت این الگوریتم (Sample size و تعداد Partition ها ) بسیار مهم است
مهمترین خاصیت »: خوشه های غیر کروی هم می تواند انجام دهد
قابلیت محاسبه big data دارد
استفاده از Partitioning
———————————————————
ارائه خانم مهندس قربانی
الگوریتم Birch
برای Big Data – استفاده از الگوریتم های ساده امکان پذیر نیست
قبلا بر اساس احتمال ( یادگیری ماشین ) و یا بر اساس آمار ( روش های فاصله ) کار می کنند.
در روشهای اماری هزینه IO خیلی زیاد است
ولی روش Birch مشکلات روش های قدیم را ندارد
تراکم خوشه ها حول جرم را نشان می دهد
اگر دو خوشه را در نظر بگیریم ۵ تا معیار داریم
با استفاده از این ها فاصله اقلیدسی یا فاصله منهتن را محاسبه کنیم
با استفاده از فرمول به فاصله خوشه ها می رسیم
یک درخت به نام CF Tree می سازد
تا بتواند خوشه ها را با هم ادغام کند
در مثال آخر LS و SS مشخص شده اند
LS : مجموع خطی داده ها ست
SS : جمع مربعات n داده هست
هر کدام از پارامتر ها یک ارتفاعی دارند
که درخت CF انها را بالانس می کند
بردار CF ذخیره می شود و داده ها ذخیر نمی شود
و با کم کردن اطلاعات داده ها از هزینه های جابجایی جلوگیری می کند
منبع : کتاب Mining of Massive Dataset
ایده کلی : تفاوت مهم Random Sampling بود
ولی birch نقاط را تبدیل به Future می کرد
Dec 092013
روش فیشر
پراکنش داده ها
داده ها را از دو بعد به یک بعئ می خواهیم map کنیم
فقط جهت بردار مهم است
معیار یا جهت مناسب ، جهتی است که جدا پذیری دو کلاس زیادباشد
و تقسیم بر پراکنش درون کلاسی هم می کنیم (که هر چه کمتر باشد بهتر است )
نام این مساله : مساله مقدار ویژه تعمیم یافته
این نمونه معمولا در امتحان می آید
یا مفهوم این که Fisher با PCA جه فرقی می کند
نمونه ای که ممکن است در امتحان بیاید
معمولا دوستان در اینورس کردن ماتریس اشتباه می کنند
جهتش هم می خواهیم که رسم کنید
——————————–
روش های خوشه بندی
فرض می کنیم دستگاهی برای دسته بندی و بسته بندی ماهی داریم
برای تفکیک ماهی ها از روش های خوشه بندی می خواهیم استفاده کنیم
اولین قدم data Gathering هست – طبقه بندی اطلاعات اولیه جمع آوری شده
خیلی از مسایل خوشه بندی تعبیر Geo metric دارند
اگر بتوانیم Rule برایش تعریف کنیم
آقای فیشر اولین بار مساله pattern Recognition را حل کرد و داده های IRIS رو مطرح کرد
قانون که می گذاریم باید برای داده های بعدی هم خوب کار کند
هر چه مدل ساده تر باشد احتمال اینکه برای داده های بعدی هم کار کند محتمل تر است
over fitting
به صورت simple از هم جدا کنیم
Predictive Accuracy
صحت پیش بینی
Accuracy صحت : تعداد صحیح ها تقسیم بر تعداد کل نمونه ها
خطا : تعداد اشتباهات تقسیم بر تعداد کل نمونه ها
روش k-fold :
داده ها را به دو قسمت تقسیم می کنیم
داده های train و داده های test
یک مدل را بر اساس داده های Train می سازیم و test را با آن آزمایش می کنیم
داده ها را به k قسمت مساوی تقسیم می کنیم
قدم اول : مدل را می سازم و با قسمت k ام خطای مدل را بدست می آوریم
قدم دوم : k-1 را Train در نظر می گیریم و باز خطا را بدست می آوریم
یک مقاله به صورت تجربی (imperical ) بخش ها را به ۱۰ قسمت تقسیم کردند
و ما هم اکثر مسایل رو ۱۰-fold می گوییم
Nearest Neighbor Classifier
هر داده جدیدی که آمد فاصله اش را با کل داده های قبلی حساب کن ، سپس sort کن
کمترین فاصله ها اکثریت را پیدا می کنیم
جزء روش های Lazy محسوب می شود چون خیلی هزینه بر هست ( با محاسباتی زیاد
هست )
جلسه بعد nearest neghbor را می گوییم
Dec 072013
خلاصه درس تدریس یار خوشه بندی – ۹۲/۰۹/۱۶
فیشر دو کلاسه را جلسه قبل گفتیم
هم واریانس بین کلاسی و هم واریانس درون کلاسی را محاسبه می کردیم
از لاگرانژ استفاده نکردیم و مستقیم مشتق گرفتیم ( چون صورت و مخرج با هم ساده می شد)
که رابطه ۴٫۲۹ بدست آمد
برای خوشه بندی کافیست روی داده ها یک میانگین های تصویر شده را محاسبه کنیم
متوسط میانگین های تصویر شده
——————————————
فیشر چند کلاسه :
مثلا روی داده های IRIS که چهار بعدی هست که می خواهیم به دو یا سه بعد کاهش می دهیم
فیشر حالت چند کلاسه – تعداد ابعاد از D بعد به به بیشتر از یک بعد و کمتر از D بعد هست
می خواهیم ‘D ویژگی خطی بدست بیاوریم
اگر ۴ بعد داریم می خواهیم به دو بعد کاهش بدهیم یعنی ‘D مساوی ۲ هست دوبردار باید داشته باشیم w1 و w2 داریم
رابطه ۴٫۳۹
S Within جمع روی k کلاس واریانس درون کلاسی
یک ماتریس نسبت به دو کلاسه بیشتر داریم به اسم :
S total ماتریس کواریانس کل نمونه ها ( پراکندگی کل داده ها صرف نظر از کلاسشون )
ماتریس کواریانس کل را می توان به صورت جمع ماتریس درون کلاسی و ماتریس بین کلاسی نوشت
متوسط هر کلاس با متوسط همه کلاس ها S Bitween
Trace : اعضای قطر اصلی را با هم جمع کنیم
برای اینکه مساله فیشر را حل کنیم Sw , Sb را باید محاسبه کنیم
S^-1w*Sb
y1 , y2 در کنار هم بردار دو بعدی کاهش یافته می شود
نکته : Rank ماتریس ( درجه ماتریس )
می خواهیم ببینیم که حداکثر به چند بعد می توانیم کاهش بدهیم
هر ماتریس درون کلاسی Rank آن ۱ است
و k تا ماتریس را که با هم جمع می کنیم Rank آن K می شود
چون تمام متوسط ها به m ربط پبدا کردند Rank k-1 می شود
پس برای IRIS به دو بعد می توانیم کاهش دهیم چون ۳ تا کلاس دارد
——————————–
تمرین : فیشر ۳ کلاسه IRIS را انجام دهید
——————————–
تمرین مهم :
موضوع اول : K-means
Search کنید در موضوعات k-means که به آن VQ یا LBG هم می گویند
می خواهیم انواع حالت های آنرا بگویید ( weighted VQ )
مقاله های جدید را پیدا کنید
۱- انواع روش های VQ را بگویند
۲- روش دوم VQ را بهبود دادند
۳- روشهای VQ را Weighted را گفته اند
Wave Distance – چه تابع هایی را می توان به جای Distance اقلیدسی ، معیار فاصله جدید استفاده کرده
به جای تابع نرم اقلیدسی چه تابع های دیگری را گذاشته است
ترجیحا مقالاتی را پیدا کنید که Cost Function های جدید ارائه کرده اند
————————————
موضوع GMM
————————————
موضوع Kernel
————————————
موضوع Fisher
Dec 012013
Nov 302013
خلاصه درس تدریس یار خوشه بندی – آقای برادران – ۹۲/۰۹/۰۹
تمرین که تا پنج شنبه ۱۴/۰۹/۹۲ تمدید شد
Fisher Linear Discriminant
جدا ساز خطی فیشر
فیشر ۲ کلاسه (C1 , C2) داریم
D بعدی هستند و می خواهیم به فضای ۱ بعدی کاهش دهیم
y=W’*X
w محور خروجی فیشر هست
y داده های تصویر شده
در جدا سازی خطی به روش فیشر، نگاشت با دید کلاسه بندی انجام می شود و شامل ۲ مرحله است :
مرحله ۱ : نگاشت در فضای D بعدی به یک بعدی یا چند بعدی
مرحله ۲ : طبقه بندی بر اساس محور های جدید
در این روش نگاشت به صورتی انجام شود که کلاس ها در دستگاه مختصات جدید متمایز هستند
(m2-m1=w'(m2-m1
m2-m1 سمت چپ میانگین داده های تصویر شده هستند
m2-m1 سمت راست میانگین داده های اصلی هستند
چون نمی توانیم m2-m1 سمت راست را تغییر دهیم بایستی w را تغییر دهیم تا m2-m1 زیاد شود
برای اینکه فاصله بین کلاس ها بیشتر باشد
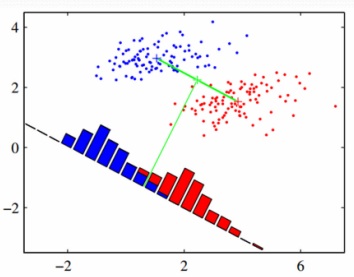
اگر واریاس را لحاظ کنیم :
پراکندکی بین دو کلاس زیاد شده
ولی پرکندگی داخل کلاس ها کم شده
که این از اهداف فیشر است
پس بهینه سازی انجام شده توسط روش فیشر :
در عین حالی که فاصله بین متوسط کلاس ها را ماکزیمم کند
واریانس درون کلاسی را هم حداقل نماید تا در حد ممکن هم پوشانی کلاس ها با یکدیگر کاهش یابد.
—————————–
– Bitween – Inter Class – ماتریس بین کلاسی Sb=(m2-m1)-(m2-m1)transpose
– Within – Intra Class ماتریس درون کلاسی
برای محاسبه w این را لحاظ می کنیم که با جهت w سر و کار داریم و نه اندازه اش
Nov 282013
دانلود کلاس ضبط شده جلسه حضوری آقای برادران پنج شنبه ۹۲/۰۹/۰۷
جزوه روز پنج شنبه ۰۷/۰۹/۹۲ که خانم مهندس صحت زحمت کشیدند
Nov 252013
خلاصه مباحث درس خوشه بندی – دکتر زارع – ۹۲/۰۹/۰۴
مبحث Kernel
و روش فیشر
نکته : یک فایل ورد یک صفحه ای Topic مقاله به همراه سال Journal بفرستید
که در موضوع کلاس باشید
تغییرات را با ماتریس کواریانس نشان می دادیم
با استفاده از تابع لاگرانژ انجام می دادیم
خلاصه PCA: اول ماتریس را Centralize می کردیم ماتریس S را می سازیم ، مقدار
ویژه و بردار ویژه را بدست می آوریم
میشه ثابت کرد اگر بخواهیم کمترین میزان Reconstruction را داشته باشیم
نگاشت تولید شده توسط PCA کمترین خطای بازیابی را می دهد
PCA یک روش Unsupervised هست
ولی روش های جدید Supervised آن هم آمده است
دقیقترین نمایش داده ها در فضای با بعد کمتر (مثل مپ کردن تصویر )
————————————–
Kernel Trick
افزایش بعد برای جدا سازی خطی
PCA را بر اساس Dot Product می خواهیم بنویسیم
کتاب Principal Component Analysis
—————————————–
بحث بعدی : fisher LDA کاهش بعد با در نظر گرفتن کلاس ها است
اشکال PCA در کاهش بعد این بود که کلاس ها با هم ترکیب می شوند
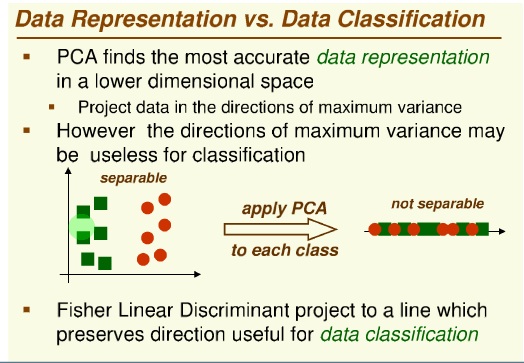
روش فیشر :
Nov 232013
فرمولاسیون ماکزیمم واریانس
بحث PCA
و بحث Kernel
ورودی مساله : N تا داد ها ی D بعدی
یک زیر فضا را می خواهیم بدست بیاوریم که بعد داده های جدید از بعد داده های اصلی
کمتر باشد.
پراکندگی داده های تصویر شده حداگثر شود
Max ( Variance )
بردار U فقط جهتش مهم بود
برای تصویر داده روی بردار ، داده را در بردار ضرب می کنیم
اگر اندازه یک برداری بزرگ باشد ، داده را که ضرب میکنیم مقدار بزرگتری بدست می آید
اگر فضای تصویر M بعدی را در نظر بگیریم
تصویر خطی بهینه ای که برای آن واریانس داده های تصویر شده بیشینه شود.
————————————————
Kernel Method
ابزار خیلی پر کاربرد در مسایل غیر خطی
در مساله که داده ها در فضا قرار گرفته اند که با یک خط نمی توانیم جدا کنیم
مثل دو تا شکل ماه که ترکیب شده اند
از یک سری منحنی های غیر خطی باید استفاده کنیم که Kernel این امکان را فراهم
میکند
Kernel داده ها را به فضایی با بعد بالاتر تصویر می کند (فضای وِیژگی)
Motivations – Kernet Definiation – Mercer’s Theorem – Kernel Matrix – Kernel
Construction
یکسری Classifier خطی داریم ، یکسری Label داریم
کلاس ضربدر و کلاس دایره
شکل سمت چپ کلاس اولیه است
اگر خطی جدا می شد روش های SVM می شد استفاده کرد
به دنبال راهی می گردیم که به صورت خطی بتوانیم جدا کنیم
داده ها را از فضای ۲ بعدی به فضای ۳ بعدی تبدیل می کنیم
روش شکل تبدیل یافته سمت راست می توانیم classifier خطی بزنیم
فضای توسعه یافته را فی می گوییم
اگر بتوانیم دو تا فی را پشت سر هم بنویسیم به جایش می توانیم تابع کرنل را جایگزین کنیم
جلسه حضوری پنج شنبه ۷ آذر
مهلت تمرین تا جمعه ۸ آذر
Nov 182013
می خواهیم بیشترین تغییرات را حفظ کنیم
تغییرات را با واریانس نمایش می دهیم
بیشترین نسبت تغییرات داخل z1
z2 دومین مولفه اصلی
مقادیر ویژه
بردار ویژه
eig(A) در متلب eigenVector و eigenValue
را به ما خواهد داد
یا SVD(A) برای هر ماتریسی یک تجزیه می
دهد
باید possitive definite باشد
از ضرایب لاگرانژ استفاده کنیم
از یک فضای p بعدی به فضای ۱ بعدی
کاهش دادیم
—————————————–
Reconstruction بازیابی
تبدیل زدیم برای کاهش بعد
ولی باید برگردانیم به فضای اولیه
PCA
برای حذف نویز در تصویر
Nov 162013
تمرین مهلت : ۴ آذر
GMM
پیاده سازی k-means
جواب خروجی های k-means بردار وزن ، کواریانس ، را به GMM می دهیم
روش PCA ( Pricipal Component Analysis)
یکی از روش های کاهش بعد هست
وقتی ابعد زیادی داریم باید از روش کاهش بعد استفاده کنیم
مثلا ۳ تا بعد را نسبت به هم رسم کنیم که حالت های خیلی زیادی می شود.
یا اینکه به صورت رندوم چند مولفه را حذف کنیم !!!
یا اینکه مولفه هایی را نگه داریم که بیشترین تاثیر گذاری را دارد
پس PCA روشی است که کاربرد های ( کاهش بعد ، فشرده سازی ، استخراج ویژگی ،تصویر سازی ) دارد
دو تعریف رایج برای PCA که الگوریتم یکسانی دارد :
تعریف ۱ : داده ها را در یک زیر فضا تصویر کنیم به طوری که هدفی آن واریانس داده های تصویر شده بیشینه باشد
تعریف ۲ : تصویر خطی که فاصله تصویر میانگین فاصله های مجذور شده بین نقاط داده های و تصویرهایشان ، کمینه شود.
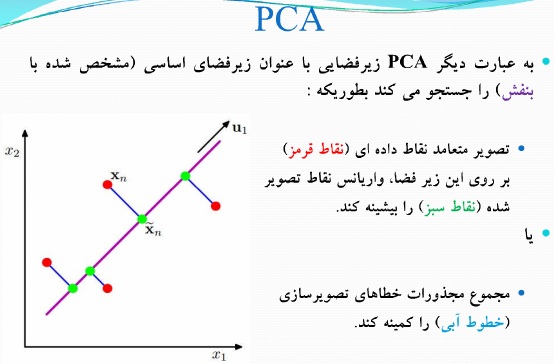
داده های اصلی داده های قرمز رنگ هستند
از این داده های قرمز رنگ تصویری رسم می کنیم که نقاط سبز بدست می آید
با تعریف اول : نقاط سبز از هم بیشترین فاصله را داشته باشند
با تعریف دوم : مجموع خط های آبی رنگ کمترین باشد
فرمولاسیون ماکزیمم واریانس :
این فرمولاسیون مطابق با تعریف اول است .
مثلا ما ۱۰۰ تا داده ۴ بعدی داریم
N=100
D=4
می خواهیم واریانس تصویر داده ها حداکثر شود
در ابتدا فرض می کنیم که داده ها را در یک بعد بهینه می خواهیم تصویر کنیم
اندازه بردار اهمیتی ندارد ، جهت بردار مهم است
پس قیدی می گذاریم : Norm بردار u1 باید ۱ شود
یا اول از کل داد ه ها میانگین بگیریم بعد تصویر کنیم
میانگین داده ها ی تصویر شده را بدست آوردیم
S ماتریس کواریانس
u هم بردار
حتما این اسلاید ها را مطالعه کنید
Nov 112013
Data matrix
N record
each record has p features
N is very large
p is very large
both of them
N no problem, p is very large
p no peoblem, N is very large
کاهش ویژگی Feature Reduction
فرض کنیم در فضای ۱۰ بعدی کار می کنیم می خواهیم بعد ها را کاهش دهیم
بر اساس مساله کار می کنند
supervised , unsupervised
minimum Information Loss
فاصله بین کلاس ها را هم بهتر است که بیشتر کنیم
x1 تا xn مشاهدات ما هستند
که فضای p بعدی ما هستند
G ماتریس تبدیل هست
داده های با حجم زیاد Hign Dimentional را باید حجمش را کم کنیم
دسته بندی
Feature Selection : اگر p تا بعد دارم فقط با فیوچر های موثر کار کنیم
Visualization
Data Compression
Noise Removal
—————-
Application of feature reduction
Face recognition
Handwrittien digit recognition
textmining
Image retrieval
Microarray Data Analysis
Protein classification
——————
Feature Reduction Algorithms :
Unsupervised :
-latent Semantinc Indexing ( LSI) : truncated SVD
– Independent Component Analysis (ICA)
PCA
CCA
Supervised :
LDA
Semi-supervised :
Research Topics
——————–
Linear
LSI
PCA
LDA
CCA : cononical Correclation
—————————–
PCA : principal Component Analysis
http://www.sas.com/data-visualization/overview.html
Nov 092013
۹۲/۰۸/۱۸
ادامه GMM
روش EM برای مخلوط های گوسی
ضرایب مولفه های گوسی
بردار میانگین
و ماتریس های کواریانس گوسی
قلب هر الگوریتم خوشه بندی cost function آن است
که به پارامتر های الگوریتم خوشه بندی می رسیم
به ما N تا بردار ویژگی میدهند یک GMM را باید به آن Fit کنیم
تشخیص تعداد خوشه ها
۱-خروجی روش k-means را به عنوان ورودی GMM ( که بردار هستند )
ضرایب مخلوط pk را چجوری می تونیم از k-means بدست بیاریم ؟
k-means یک الگوریتم هارد هست و هر نقطه را فقط به یک خوشه اختصاص می دهد
ماتریس کواریانس = بردار ویژگی منهای متوسط ضرب در ماتریس ترانهاده
وزن ها : تعداد اعضای هر خوشه تقسیم بر تعداد کل
——————–
ورودی و خروجی GMM چه چیز هایی هستند ؟
ورودی : N تا بردار ویژگی
خروجی : پارامتر های مخلوط گوسی
برای این داده ها مدلی را فیت می کنیم که داده ها را توصیف می کند
نکته : پارامتر های GMM را نمی توانیم در اول کار محاسبه کنیم ( فرم بسته ندارد )
پس یک سری فرمول غیر بسته ای که بدست آوردیم تابع درست نمایی را محاسبه می کنیم و مداوما تکرار می کنیم تا دیگر تغییر نکند
ماتریس قطری ایزوتوپریک
a) خوشه بندی بر اساس رندوم گرفته
b ) در مرحله دوم : مقدار احتمال پسین را پیدا کرده
c) قسمت maximation را انجام دادیم ( متوسط ها، وزن ها ، … )
d) دوباره احتمال پسین انتخاب کردیم
e) دوباره پارامتر های توزیع پسین را انتخاب کردیم ( در مرحله پنجم )
f) مرحله بیست که تابع درستنمایی تغییر نمی کند
Nov 042013
خلاصه درس خوشه بندی ۹۲/۰۸/۱۳ دکتر زارع
ادامه بحث social Network
یک سری Object داریم که به هم متصل هستند
بزرگترین گراف همبند = Giant Component
Network crowd and marketing
kleinburg , jon
Community Structure یا Community detection
مفهومی هست به نام Clustering Coefficent ضریب خوشه بندی
Zacharay Karate Club
شبکه ای به عنوان Bench mark شناسایی جوامع پنهان هست
این شبکه دو بخش است
یک باشگاه – یک مربی و تعدادی هنر آموز
مربی به یک باشگاه دیگر می رود
Scientometric :به دنبال این است که شاخه مختلف علم چه ارتباطی می توان داشته باشد
و پیش بینی اینکه یک دانش جدید کجا بوجود می آید.
: information retreival
Determining Weights
Edge independent path
Nov 022013
خلاصه درس تدریس یار خوشه بندی – مهندس برادران
پارامتر گاما z k
متغیر تصادفی است که نسبت داده می شود به خوشه k ام
احتمال پیشین : پیش از اینکه x وجود داشته باشد ، فقط احتمال پیشین می دهیم
تابع توزیع نرمال
مرکز یک توزیع نرمال محلی است که بیشترین چگالی داده وجود دارد
خوشه بندی با GMM
فرض کنیم یک GMM 3 مولفه ای را برای خوشه ها کافی است
استفاده از فقط liklihood – بردار x را اگر در هر گوسی بگذاریم و عدد بزرگتری را بدهد می گوییم مربوط به همان خوشه است
اگر پارامتر پسین هم داشته باشیم ، ممکن است در Prior هر خوشه هم ضرب کند.
اگر صورت کسر بیشتر بود تاثیری بر مخرج کسر ندارد
مخرج در خوشه بندی تاثیر ندارد
جمع prior ها در تابع GMM مساوی ۱ است
برای اینکه نرمال سازی انجام دهیم تقسیم می کنیم
چون احتمال پسین جمعش باید ۱ باشد
آیا جمع likelihood هم باید ۱ باشد ؟ خیر ، چون ممکن است داده های پرتی داشته باشیم که احتمال آن برای مرتبط شدن به هر خوشه ای بسیار کم باشد.
مهمترین رابطه GMM
[image1]
با فرض iid بودن داده ها (مستقل و یکسان )
کل داده ها را با X نمایش می دهیم
لگاریتم
log a + log b
ضرب لگاریتم که پشت خط هستند میشه جمع لگاریتم ها شون
اگر در GMM مشتق بگیریم به رابطه بسته نمی رسیم بنابراین EM ارائه شد
تابع likelihood
مشتق نسبت به میو کا ( متوسط یک خوشه مشتق می گیریم )
برای خوشه بندی یک تابع Cost تعریف می کنیم که در اینجا تابع likelihood است
Nk یک عدد اعشاری است
– ماکزیمم سازی بدون قید
– ماکزیمم سازی مقید
Oct 282013
خلاصه درس خوشه بندی – دکتر زارع – ۹۲/۰۸/۰۶
امتحان هفته بعد میانترم نیست
در حد روشهای سلسله مراتبی و مباحث اولیه خوشه بندی – مثل نمونه سوالی که دادیم
هفته بعد امتحان میان ترم نیست
یا اینکه یک تمرین بدهیم
بحث Model Selection
Social Network
Intruduction to Social Networks
Jure Leskoves
Stanford University
مهندسی سامانه های شبکه ای
علم جدید در قرن ۲۱ هست
Big Data
Data Science
سال ۱۹۶۴ آزمایش ارسال ۱۰۰ بسته پستی به آمریکا انجام شده که حداکثر با ۶ لینک این کار انجام شده
پدیده Small World
بخشی از این را فیزیکدانان و بعد ریاضی دانان و بعد کامپیوتری ها به دنبال نتیجه گیری از شبکه های اجتماعی هستند
۶ Degree of seperated
کتاب Networks an introduction m e j newman
یک گراف کشیده از ارتباطات اینترنت
Connection Between political blogs
http://connectedthebook.com/
Networks : Organizations
ارتباط ها را با یالها نمایش می دهیم
شبکه اقتصادی
مغز انسان
Human Brain 10 -100 billions neurons
https://www.humanbrainproject.eu/
شبکه زیستی پروتئین ppi
شبکه متابولیک
برای فهم ارتباطات شبکه :
Empirical : پرسشنامه ای
Mathematical ریاضی
Algorithms الگوریتمی
اولین مدل های شبکه ای را به روش ریاضی erdus , و reny ارائه دادند
جچوری به این مدلهای برسیم
یک سری pattern و خواص آماری و یک سری معیار باید بتوانیم استخراج کنیم
مدل ها را استخراج کنیم
و بفهمیم که شبکه ها چرا اینگونه ساخته شده اند
اقای ves vigiani – complex network بحث بخش ویروس های کامپیوتری را تشخیص داد ، رفتار دینامیک
شبکه ها برای دسترسی پذیری به اطلاعات ، جهانی شدن
Networks : Impact
Dotnet Bilioners
معرفی شبکه
ارتباطهای بیماری ها به هم
Networks Really Matter
Network یک کلکسیونی از اشیا مختلف هست که به هم وصل شده اند
Objects : Node , Vertices
Intractions : Links , edges
System : Network , Graph
نظریه گراف : نمایش ریاضی
برای تحلیل شبکه از گراف استفاده می کنیم
نمایش صحیح برای شبکه
در برخی جاها می توان نمایش یکتا ارائه داد
شبکه های جهت دار یا بدون جهت
شبکه می تواند connected باشد می تواند Disconnected هم باشد .
دوستانی که مقاله فرستاده بودند ،امشب خوانده می شود
ISI جدید باشد